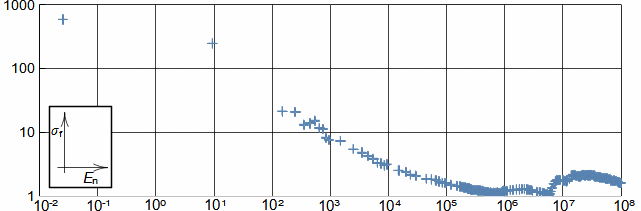
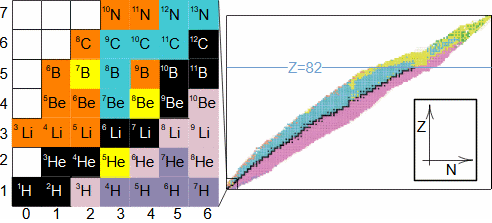
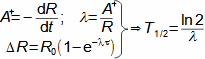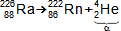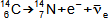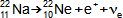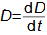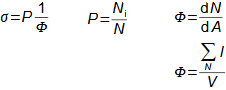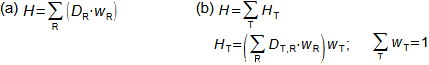engineering-sciences.education
23.

RADIOAKTIVITA A IONIZUJÍCÍ ZÁŘENÍ

23.3 . . . . . . . . . . . . . .
Radioaktivita
Historické poznámky – Radionuklidy – Kinetická energie – Aktivita
23.6 . . . . . . . . . . . . . .
Druhy radioaktivních přeměn a jejich produkty
Alfa přeměna – Beta přeměna – Pozitronová přeměna – Neutronová přeměna – Samovolné štěpení – Izomerický přechod
23.8 . . . . . . . . . . . . . .
Fyzikální účinky ionizujícího záření
Historické poznámky – Dávka záření – Ionizace – Jaderné reakce – Účinný průřez interakce
23.13 . . . . . . . . . . . . . .
Účinky ionizujícího záření na lidský organismus
Ekvivalentní dávka – Biologické účinky – Léčebné účinky
23.17 . . . . . . . . . . . . . .
Úloha 1: Výpočet efektivní ekvivalentní dávky
Úloha 2: Výpočet snížení energie gama záření po průchodu lidským tělem
23.18 . . . . . . . . . . . . . .
Odkazy
23.19 - 23.23 . . . . . . . .
Přílohy
X . . . . . . . . . . . . . . .
Doplňkový mediální obsah
Zobrazení v PDF
engineering-sciences.education 
23.2
autor:
ŠKORPÍK, Jiří – LinkedIn.com/in/jiri-skorpik
datum vydání:       
Leden 2024; Leden 2025 (2. vydání)
název:
Radioaktivita a ionizující záření
web:
engineering-sciences.education
provenience:
Brno (Česká republika)

Copyright©Jiří Škorpík, 2024-2025
All rights reserved.

 Kapitola: Radioaktivita
23.3

Radioaktivita

Radionuklid

Radioaktivní přeměna

Jaderný izomer

Ionizace

Radioaktivita je vlastnost některých druhů atomových jader samovolně se přeměňovat, takové druhy jader se nazývají radionuklidy (respektive radioizotop daného prvku). Při radioaktivní přeměně se změní složení jádra atomu a uvolní energie ve formě kinetické energie produktů této přeměny. Těmito produkty mohou být atomové elementární částice, fotony i jádra lehčích prvků. Existují i případy radionuklidů, kdy při radioaktivní přeměně nedojde ke změně složení jádra, ale pouze ke snížení jeho energetického obsahu a vyzáření fotonu, taková jádra nazývané jadernými izomery. Počet radioaktivních přeměn za vteřinu ve vyšetřovaném vzorku hmoty označujeme jeho aktivitou. Produkty radioaktivních přeměn lze detekovat, protože jsou schopny atomy prostředí, kterým je vzorek obklopen, proniknou, ionizovat, respektive energeticky ovlivnit.

Historické poznámky

Marie Curie-Skłodowská

Pierre Curie

Antoine H. Becquerel

Radioaktivita

Objevitelé radioaktivity byly hned tři vědci pracující společně, francouzská vědkyně polského původu Marie Curie-Skłodowská (1867-1934), francouzský fyzik a chemik Pierre Curie (1859-1906) a především francouzský fyzik Antoine H. Becquerel (1852-1908) [Běhounek, 1945]. Hlavní přínos prvních dvou je, že dokázali izolovat prvky, které prokazatelně vykazovaly aktivitu v podobě ionizujícího záření od těch bez této aktivity – přitom objevili nové prvky Polonium a Radium. Také zavedli výraz radioaktivita. Becquerel ještě před nimi pozoroval ionizující záření některých nerostů (tím inspiroval oba manželé Curie v jejich směru).

Radionuklidy

Každý známý prvek má izotopy, jejichž atomová jádra obsahují počet protonů odpovídající danému prvku označovaném jako protonové číslo. Toto číslo je pro daný prvek neměnné, nicméně každý prvek má několik izotopů odlišujících se počtem neutronů v jádře, označovaném jako neutronové číslo. Na počtu protonů v jádře závisí, zda je daný izotop radioaktivní či nikoliv, přičemž každý prvek do protonového čísla 82 (olovo) má mimo radioizotopů také alespoň jeden izotop stabilní (neradioaktivní). Na Obrázku 1 je tabulka všech známých prvků a jejich izotopů tj. do protonového čísla 117. Na každém řádku jsou vypsané do buněk tabulky jednotlivé známé izotopy daného prvku, přičemž číslo řádku odpovídá protonovému číslu tohoto prvku a číslo sloupce tabulky odpovídá počtu neutronů v jádře. Buňky s černým pozadím označují stabilní izotop, to znamená, že izotopy ve světlých buňkách jsou radioizotopy daného prvku.

 Kapitola: Radioaktivita
23.4
Tabulka prvků a jejich izotopů
1: Tabulka prvků a jejich izotopů
Z [-] protonové číslo; N [-] neutronové číslo. Horní index u značky prvku označuje nukleonové číslo (součet protonů a neutronů v jádře). Barvy jednotlivých izotopů označuje druh radioaktivní přeměny, viz. následující kapitola. Obrázek vpravo je převzat z [Wikimedia Commons].

Přirozené radionuklidy

Umělé radionuklidy

Výše uvedení vědci pozorovali radioaktivitu přírodních radionuklidů a jednotlivé prvky získávali na základě rozdílných chemických vlastností z přírodních nerostů. Na povrchu Země se vyskytují atomy radionuklidů ve velmi malých koncentracích, takže takto získaný radioaktivní materiál byl jednak v malém množství jednak byl drahý, proto se ho využívalo pouze pro vědecké účely a lékařské (rentgen, radioterapie..). Dnes většinou získáváme potřebné množství radionuklidů uměle jako vedlejší produkty při jaderných reakcích.

Kinetická energie

Použité jaderné palivo

Radioizotopový generátor

Produkty radioaktivních přeměn mají kinetickou energii, která se maří uvnitř látky vzájemnými srážkami, což se navenek projeví ohřevem. Zahřívní látky při radioaktivních přeměnách je problém například při skladování radioaktivních látek a především použitého jaderného paliva z jaderných elektráren [Škorpík, 2022]. Naopak teplo z radioaktivních přeměn je využíváno v radioizotopových generátorech, ve kterých se toto teplo využívá pro výrobu tepla či elektřiny například u strojů určené pro práci mimo Zemi.

 Kapitola: Radioaktivita
23.5

Aktivita

Becquerel

Přeměnová konstanta

Poločas přeměny

Ve vyšetřovaném vzorku radionuklidů můžeme sledovat jejich radioaktivní přeměny, přitom počet radioaktivních přeměn za vteřinu označujeme veličinou aktivita, jejíž značkou je Becquerel. Protože pravděpodobnost radioaktivní přeměny jednotlivých nuklidů je stejná, tak podíl aktivity a počtu radionuklidů ve vzorku bude konstantní – tento poměr se nazývá přeměnová konstanta radionuklidu. Například je-li přeměnová konstanta vzorku rovna 1·10-2 s-1, pak to znamená, že vzorku každou vteřinu proběhne radioaktivní přeměna u 1 % z přítomného počtu radionuklidů. Doba, za kterou ve vyšetřovaném vzorku proběhne radioaktivní přeměna přesně u poloviny atomů se nazývá poločas přeměny, která je definována Vzorcem 2.

Aktivita, přeměnová konstanta a výpočet úbytku radioaktivních jader
2: Aktivita, přeměnová konstanta a výpočet úbytku radioaktivních jader
λ [s-1] přeměnová konstanta; A+ [1·s-1; Bq] aktivita (počet radioaktivních přeměn za vteřinu); R [-] počet přítomných atomů radionuklidu – dR tedy znamená úbytek počtu přítomných radionuklidů v důsledku radioaktivních přeměn jeho jader; T1/2 [s] poločas přeměny; n [mol] látkové množství atomů radionuklidu; NA [mol-1] Avogadrova konstanta; ΔR [-] úbytek počtu radioaktivních jader ve vyšetřované množině; R0 [-] počet radioaktivních jader na počátku sledování; τ [s] doba, která uplynula od počátku sledování. Vzorec pro výpočet úbytku radioaktivních jader ve vyšetřovaném souboru je odvozen v Příloze 3.

Poločas přeměny

Poločas přeměny je statistickou veličinou odvozenou pro velký soubor atomů radionuklidu, takže v případě dvou atomů radionuklidu automaticky neplatí, že u jednoho z nich dojde po uplynutí poločasu přeměny k radioaktivní přeměně se 100% pravděpodobností, ale 50% pravděpodobností atd.

Tritium

Poločas přeměny

Poločasy přeměny některých radionuklidů jsou tak krátké, že je v přírodě nenajdeme, protože jejich jádra se rozpadla. Například izotop vodíku tritium má poločas přeměny přibližně 12,32 let. Velmi krátký poločas přeměny je hlavní problém při výrobě těžších prvků. Ty se obvykle vyrábí tak, že se do jádra těžkého radioaktivního izotopu přidávají protony a neutrony, přitom tento proces musí být výrazně rychlejší než poločas přeměny.

Neutron

Proton

Elektron

Přeměnám podléhá i volný neutron, jeho střední délka života mimo jádro je 877,75 +/- 0,34 s [Gonzalez, 2021]. Rozpadá se na proton a elektron. U volných protonů a volných elektronů zatím nebyl zaznamenán samovolný rozpad.

 Kapitola: Druhy radioaktivních přeměn a jejich produkty
23.6

Druhy radioaktivních přeměn a jejich produkty

Ernest Rutherford

K definitivní potvrzení toho, že existuje více druhů radioaktivních přeměn přispěl výzkum britského fyzika novozélandského původu Ernesta Rutherforda (1871-1937). Ten potvrdil existenci dvou druhů, které označil α, β přeměnou podle zachycených produktů radioaktivních přeměn, respektive ionizujícího záření. Přičemž přeměna jednoho izotopu může být zdrojem i více jak jednoho druhu záření, ale obvykle jeden druh převažuje. Později byly objeveny další druhy radioaktivních přeměn jako pozitronová přeměna, neutronová přeměna, samovolné štěpení a izomerický přechod. Na Obrázku 1 jsou radionuklidy odlišeny podle typu přeměny, ale některé radionuklidy mohou podléhat více typům radioaktivních přeměn s různou pravděpodobností. Přesné údaje o radioaktivních přeměnách jednotlivých radionuklidů lze nalézt v tabulkách, například [Hála, 1998].

Alfa přeměna

Radium Ra

Radon Rn

Helium He

α-záření

α-přeměna se vyskytuje u radioaktivních nuklidů těžkých prvků, kde se v jádru projevuje silné odpuzování protonů (nízký podíl neutronů). Při této přeměně jádro emituje (vyzáří) jádro helia, Vzorce 3. Jádro Helia je současně částice α-záření. Radionuklidy podléhající převážně α-přeměně jsou označeny na Obrázku 1 žlutě.

Příklad α přeměny
3: Příklad α-přeměny
α-jádro helia, též částice α-záření.

Beta přeměna

Transmutace

Radiokarbonová metoda

Uhlík C

Dusík N

Elektron

β-záření

Antineutrino

Při β--přeměnách jsou vyzářeny z jádra elektrony. β- přeměna vzniká při přeměně neutronu v jádře radionuklidu na proton. Této přeměny, respektive transmutace, se využívá k datování úmrtí organismu pomocí radiokarbonové metody, kdy se využívá β přeměny podle Vzorce 4. Radionuklid 14C vzniká v horních vrstvách atmosféry reakcí kosmického záření s dusíkem. Tento radionuklid se prostřednictvím molekuly CO2 dostává do živých organismů. Díky metabolismu organismu se uhlík v organismu vyměšuje a zase přijímá. Po odumření organismu se tato výměna zastaví a radionuklid 14C se rozpadá s poločasem přeměny 5730 let na izotop dusíku 14N podle uvedené rovnice. Z poměru obsahu izotopů 14C a 14N v odumřelém organismu lze tedy určit dobu, kdy organismus zemřel. Radionuklidy podléhající převážně β-přeměně jsou označeny na Obrázku 1 růžově.

 Kapitola: Druhy radioaktivních přeměn a jejich produkty
23.7
Příklad β<sub>-</sub> přeměny
4: Příklad β--přeměny
ν-e-antineutrino.

Pozitronová přeměna

Sodík Na

Neon Ne

Pozitron

Neutrino

Mimo přeměny-β-, kdy se uvolňuje z jádra elektron se vyskytuje i přeměna-β+, kdy se uvolňuje z jádra kladně nabitý elektron, nazývaný pozitron. Tento typ přeměny se vyskytuje u umělých radionuklidů. Vzniká při přeměně nadbytečných protonů v jádře na neutron, elektron a neutrino, například podle Vzorce 5. Radionuklidy podléhající převážně pozitronové přeměně jsou označeny na Obrázku 1 modře.

Příklad β<sub>+</sub> přeměny
5: Příklad β+-přeměny
e+-pozitron – opačně nabitý elektron (částice β+-záření); νe-neutrino.

Neutronová přeměna

Neutronová přeměna s vyzářením neutronu z jádra je typická pro radionuklidy s velkým přebytkem neutronů oproti stabilnímu stavu. Například vodík 6H přechází neutronovou přeměnou na vodík 5H. Radionuklidy podléhající převážně neutronové přeměně jsou označeny na Obrázku 1 fialově.

Samovolné štěpení

Samovolné štěpení je typické pro velmi těžké jádra radionuklidů, které se mohou roštěpit bez vnějších zásahů na dvě lehčí jádra. Samovolné štěpení bylo objeveno v roce 1940 sovětskými fyziky Georgijem Fljorovem (1913-1990) a Konstantinem Petržakem (1907-1998). Z principu samovolného štěpení mohou být jeho produkty alfa záření, protony, neutrony, což se označuje jako emise nukleonů. Radionuklidy podléhající převážně samovolnému štěpení jsou označeny na Obrázku 1 zeleně.

Izomerický přechod

γ-záření

Jaderný izomer

Za izomerický přechod jádra je považováno energetické přeskupení nukleonů, které zahrnuje i vyzáření fotonu s energiemi v řádech vyšších jak 104 eV. Přičemž tato změna přichází po některé jiné radioaktivní přeměně jádra s takovým zpožděním, že tento přechod je považován za samostatnou událost s vlastním poločasem přeměna. V tabulkách se jaderný izomer obvykle označuje písmenem-m u nukleonového čísla. Jaderné izomery se používají jako zdroje fotonů u zobrazovacích metod, zejména ve zdravotnictví, viz Úloha 2.

 Kapitola: Fyzikální účinky ionizujícího záření
23.8

Fyzikální účinky ionizujícího záření

Tok subatomárních částic, které vznikají nejen při radioaktivních přeměnách, neboli záření, mohou elektronové obaly atomů a molekul prostředí, do kterého pronikají, ionizovat případně mohou pronikat až k atomovým jádrům a ty excitovat a tedy přivést k jaderné reakci. Tyto interakce částic záření a prostředí se navenek projeví zvýšením energetického obsahu prostředí a snížením energetického obsahu záření nebo jeho úplným pohlcením uvnitř prostředí. Veličina, která udává množství pohlcené energie vyšetřovaného prostředí se nazývá dávka záření. Veličina používána k vyhodnocení očekávaných interakcí ionizujícího záření v daném prostředí se nazývá účinný průřez interakce.

Historické poznámky

Sluneční záření

Wilhelm Röntgen

Gama záření

Foton

Přirozeným ionizujícím zářením je sluneční světlo. Sluneční světlo mění například barvu bílého papíru (fotochemická tvorba fotografie je založena na ionizačních vlastnostech viditelného světla). Sluneční světlo dokáže rozkládat slabé chemické vazby některých léků – proto jsou baleny do tmavých lahviček – apod. Proto, až do roku 1895, bylo záření spojováno s viditelností. Toho roku přišel velký zlom ve vnímání záření objevem německého fyzika Wilhelma Conrada Röntgena (1845-1923), který objevil "neviditelné" záření. Přesněji při experimentech se skleněnou výbojkou objevil záření, které dnes označujeme jako gama záření, která má ovšem stejnou podstatu jako sluneční záření neboť se jedná o tok fotonů, ale s mnohem větší energii. Později, v souvislosti s radioaktivními přeměnami byly objeveny další typy záření, respektive jejich částic.

Přírodní zdroje

Umělé zdroje

Kosmické záření

Ionizace atmosféry

Nejčastějším zdrojem ionizujícího záření bývají radioaktivní přeměny na Zemi (přírodní i umělé) a kosmické záření přicházející z okolního vesmíru, které vyzařují hvězdy a jiné aktivní útvary po zhroucení hvězd a naše Slunce. Tento mimozemský zdroj záření objevil Německý fyzik Victor Franz Hess v roce 1912, který pozoroval ionizaci vzduchu, která rostla s nadmořskou výškou. Mezi kosmické záření patří i slabé reliktní záření pocházející z období vzniku vesmíru. Kosmické záření je z drtivé většiny zachyceno elektromagnetickým polem Země a molekulami atmosféry Země, proto je ve vyšších vrstvách atmosféry tolik iontů [Atkins, 2005, s. 25].

 Kapitola: Fyzikální účinky ionizujícího záření
23.9

Dávka záření

Gray

Prostředí, které pohltí ionizující záření získá energii ε [J], což je energie sdělená látce. Dávka záření je veličinou vyjadřující velikost sdělené energie na 1 kg látky. Jednotkou dávky záření je 1 Gy (Gray), přičemž 1 Gy znamená energii 1 joulu absorbovanou 1 kg látky, viz Vzorec 6.

Dávka záření
6: Dávka záření
D [J·kg-1, Gray] dávka záření; ε [J] energie sdělená látce; m [kg] hmotnost látky.

Dávkový příkon

Rychlost s jakou je energie látce sdělována vyjadřuje dávkový příkon, viz Vzorec 7.

Dávkový příkon
7: Dávkový příkon
D [Gy·s-1; W·kg-1] dávkový příkon; t [s] čas.

Ionizace

Elektronový obal

První ionizační energie

Foton

Kationt

Disociace

Objevených ionizujících interakcí je velké množství a záleží na částici záření a její energii. Energie elektronů i hybností v elektronovém obalu jsou kvantovány, tj. svůj energetický stav mění skokově, a energie dodaná v ionizační částicí musí mít přesně takovou energii, která je potřeba k danému energetickému skoku, v opačném případě k dané interakci nemůže dojít. Například na Obrázku 8 jsou vyznačeny tzv. první ionizační energie prvků, respektive se jedná o energii fotonu potřebnou k vyražení prvního elektronu z plně zaplněného elektronového obalu – atomu s chybějícím elektronem v obalu se říká kationt. Dále existuje druhá ionizační energie (která je vyšší) pro vyražení druhého elektronu z obalu atd. Podobně ionizační energie mají i elektronové obaly chemických sloučenin – v takovém případě vede jejich ionizace k rozpadu neboli disociaci sloučeniny.

Porovnání prvních ionizačních energií jednotlivých prvků
8: Porovnání prvních ionizačních energií jednotlivých prvků
 Kapitola: Fyzikální účinky ionizujícího záření
23.10
U [eV] ionizační energie prvku. Jedná se o ionizační energie prvků pro případ základního energetického stavu daného atomu (minimální energie elektronů), kterých má každý prvek také několik možných a platí, že se zvyšujícím energetickým stavem atomu klesá ionizační energie.

Comptonův jev

Ramanův rozptyl

Braggova křivka

Pravděpodobnost, že foton bude mít přesně takovou energii jaká je potřeba k ionizaci se zdá velmi malá, nicméně při průchodu fotonu látkou není jediný druh interakce, kterou kvantová povaha rozložení energie umožňuje. Další typem interakce je kvantový rozptyl neboli Comptonův jev, při kterém se foton od elektronu (nebo atomu–ohřev) odrazí, ale přitom mu předá jen možné kvantum své energie, takže od odrazu má o to nižší energetický obsah. Dalším významnou fotonovou interakcí s elektronovým obalem je Ramanův rozptyl, při kterém elektronový obal pohltí foton o jiné energie, než odpovídá kvantovému rozdílu energií elektronu – proto ihned dojde k vyzáření fotonu jehož energie odpovídá rozdílu mezi vyšší energetickou hladinou elektronu a energií fotonu. Dokonce se může stát, že po takové interakci je vyzářen foton o vyšší energii než původní foton a elektron poklesne do nižší energetické hladiny. Ve výsledku foton při průletu prostředím může provést několik interakcí s postupným snižováním své energie, přičemž křivka závislosti předaného množství energie ionizujícího záření na vzdálenosti se nazývá Braggova křivka, viz Obrázek 9.

Braggova křivka pro foton a proton v zasažené tkáni
9: Braggova křivka pro foton a proton v zasažené tkáni
(a) křivka pro foton o energii 6 MeV; (b) křivka pro proton o energii 250 MeV. l [cm] vzdálenost od okraje tkáně; E [%] ztráta energie protonu (absorbovaná energie tkání), ztráta je vztažena k tzv. Braggově vrcholu, což je vzdálenost, na které ztratí částice maximum energie. Data z Wikimedia Commons.

Pronikavost

Alfa záření

Beta záření

Gama záření

Z posledního obrázku je také patrné, že ionizační záření pronikající prostředím i když toto prostředí ionizuje, tak jim může proniknout. Například alfa záření je zcela pohlceno až 10 cm vrstvou vzduchu, beta záření je zcela pohlceno až 20 cm vrstvou vzduchu (jeho pronikavost je větší než u α-záření) a energie gama záření (o energii fotonů větší jak MeV) se sníží na 10 000 000-1 původní úrovně až po průchodu 35 cm vrstvou olova [Něstěrenko a kol, 1959, s. 97]. Proto je γ-záření vhnodnější pro zobrazovací metody v lékařství než alfa a beta záření, která jsou tělem pohlcována (viz Úloha 2) a nevytvoří kontrast na výsldném snímku.

 Kapitola: Fyzikální účinky ionizujícího záření
23.11

Aniont

Mimo fotonů mohou s elektronovým obalem a molekulami interagovat nabité částice jako elektrony, pozitrony, protony a atomová jádra. Elektrony o určité rychlosti mohou vytvářet z neutrálních atomu záporně nabitý aniont, energie elektronu, která je k tomu potřeba se nazývá elektronová afinita. Kladně nabité částice mohou naopak elektrony s elektronových obalů vytrhávat a vytvářet své vlastní elektronové obaly apod.

Jaderné reakce

Radioaktivní materiál

ITER

Pohlcením částice ionizujícího zářením se z jádra může stát radioizotop daného prvku, nebo může transmutovat na radioaktivní izotop jiného prvku. Obvykle takto vytvořené radioizotopy mají krátký poločas rozpadu. Například materiály termonukleárního reaktoru ITER, které se stanou po provozu radioaktivní, byly vybrány tak, aby vzniklé radioizotopy měly poločas rozpadu v řádech desítek let, takže zhruba po sto letech by měly být neradioaktivní a bylo by možné je recyklovat.

Nejznámější jadernou reakcí je štěpení jádra neutronem, viz článek Jaderná energie a technologie pro její využití [Škorpík, 2024]. V případě lehkých jader může dojít i k jaderné fúzi, která je také popsána v článku uvedeném výše.

Účinný průřez interakce

Podmínky interakce

Fluence

Částice ionizujícího záření vstupující do vyšetřovaného objemu (prostředí) tedy může v tomto objemu způsobit některou z výše uvedenou událost. Míra splnění podmínek potřebných k tomu aby daná částice (střela) interagovala s částicemi uvnitř prostředí ve tvaru koule, ke kterému míří se nazývá účinný průřez interakce σ (například účinný průřez pro záchyt neutronu apod.). Účinný průřez interakce je součin pravděpodobnosti P, že nastane očekávaný druhu interakce střely a plochou terče připadající na jednu střelu (Vzorec 10). Velikost terče odpovídá ploše průřezu koule velikosti jader atomů, atomů a molekul případně tkání ve tvaru koule ku počtu střel, které za vyšetřovanou dobu k tomuto terči směřují. Převrácená hodnota plochy terče se nazývá fluence Φ (Vzorec 10). Pro větší kulové objemy prostředí, ke kterým za sledovanou dobu míří N počet střel se fluence počítá jako podíl trajektorií těchto střel ve vyšetřovaném kulovém prostředí a objemu tohoto prostředí. Nicméně výpočet fluence je někdy obtížný a zvláště u tkání diskutabilní, viz Úloha 2. Ve výsledku by hodnota účinného průřezu měla klesat s počtem střel potřebné k vyvolání očkávané interakce.

 Kapitola: Fyzikální účinky ionizujícího záření
23.12
Účinný průřez interakce
10: Účinný průřez interakce
σ [m2] účinný průřez interakce; P [-] pravděpodobnost, že daná částice způsobí interakci; N [-] počet částic směřující do prostoru možné interakce během sledovaného období; Ni [-] počet částic, které způsobí interakci; Φ [m-2] fluence; A [m2] plocha průřezu vyšetřovaného kulového objemu; V [m2] vyšetřovaný objem ve tvaru koule; l délka trajektorie jedné částice prolétávající skrz vyšetřovaný objem.

Historická poznámka

Veličina účinný průřez interakce vznikla v době projektu Manhattan, respektive při vývoji atomové bomby. Vědci v té době hledali parametr, kterým by pokryli vliv velikosti štěpitelného jádra a pravděpodobnosti, že při zachycení neutronu tímto jádrem dojde ke štěpení. Současně zavedli jednotku účinného průřezu barn, přičemž 1 barn odpovídá hodnotě 10-28 m2, což je hodnota, která odpovídá účinnému průřezu 235U pro štěpení neutronem o vysoké energii, viz Obrázek 11.

Účinný průřez 235U pro štěpení neutronem
11: Účinný průřez 235U pro štěpení neutronem
σf [barn] účinný průřez 235U pro štěpení (fission cross section); En [eV] energie neutronu (první hodnota 0,253·10-1 je energie tzv. termického neutronu, který je v kinetické rovnováze s okolními molekulami). Zdroje dat International Atomic Energy Agency - Nuclear Data Section.

Účinné průřezy pro jednotlivé typy interakcí je možné sčítat, pokud očekáváme, kteroukoliv z nich. Například foton v prolétávající prostředím s ním může interagovat různými způsoby, viz výše. Takže celkový účinný průřez pro jakýkoliv typ interakce bude součtem dílčích účinných průřezů.

 Kapitola: Účinky ionizujícího záření na lidský organismus
23.13

Účinky ionizujícího záření na lidský organismus

Deterministické účinky

Stochastické účinky

Obdržené dávky ionizující záření představuje pro lidské tělo zdravotní riziko. Ionizující záření na úrovni jednotlivých částic může způsobit různé úrovně poškození buňky i její smrt. Při abnormálně vysokých dávkách (získaných například v důsledku blízkých výkonných jaderných událostí) se projevuje i samotné zvýšení energie lidského těla popáleninami a nebo dokonce i odpařením celého těla. Navenek se může projevit obdržená dávka ionizujícího záření jako bezprostřední nemoc z ozáření (popáleniny, nevolnost atd.), pak hovoříme o tzv. deterministických účincích. Nebo za velmi dlouhou dobu, to znamená, že po ozáření je člověk naprosto zdravý, ale například po letech se u sledované skupiny osob zvýší některé druhy onkologických onemocnění nebo se nějaké zvýšený výskyt těchto onemocnění projeví až u další generace, pak hovoříme o tzv. stochastických účincích. Nicméně existují i případy, kdy lze ionizující záření použít i k léčbě. Veličina, pomocí které určujeme rizika spojené z obdrženou dávkou se nazývá ekvivalentní dávka.

Ekvivalentní dávka

Efektivní ekvivalentní dávka

Radiační váhový faktor

Sievert

Biologický účinek radiační dávky závisí jak na druhu zasaženého organismu (tkáně) tak na druhu záření. Pro vyhodnocení účinků ionizujícího záření na lidský organismus byla zavedena porovnávací veličina zvaná efektivní ekvivalentní dávka (též efektivní dávkový ekvivalent). Efektivní ekvivalentní dávka je přepočítaná dávka od jednotlivých druhů ionizujících záření na ekvivalentní dávku obdrženou ve fotonovém záření způsobující stejnou škodu na lidském těle, viz Úloha 1. Efektivní ekvivalentní dávka má jednotku 1 Sievert [Sv; J·kg-1] a je definována Vzorcem 12a, platný pro případ, že každý orgán lidského těla obdržel stejnou dávku DT.

Ekvivalentní dávka
12: Ekvivalentní dávka
H [Sv] efektivní ekvivalentní dávka (lidské tělo obdrželo dávku rovnoměrně); HT [Sv] ekvivalentní dávka konkrétní tkáně v lidského těla (equivalent dose); wR [1] radiační váhový faktor, viz Tabulka 13; wT [-] tkáňový váhový faktor (Tissue weighting factor). T-označení pro danou tkáň lidského těla; R-označuje jednotlivé druhy ionizujícího záření
 Kapitola: Účinky ionizujícího záření na lidský organismus
23.14
druh záření WR druh záření WR
fotony a elektrony všech energií 1 neutrony 3 keV-1 MeV 2,5-20
protony všech energií 2 neutrony 1 MeV-3 GeV 20-2,5
neutrony 1 eV-3 keV; <3 GeV 2,5 α záření 20
13: Radiační váhové faktory
wR [1]. [Valentin et al., 2007, s. 64].

Deterministické účinky

Stochastické účinky

Prahová ekvivalentní dávka

Zhoubný nádor

Na základě dlouhodobých pozorování účinků ionizujícího záření na lidský organismus lze stanovit oblast deterministických účinků. První případy deterministických účinků se objevují při ozáření kolem hodnot 100 mSv u 1-5 % ozářených osob. Tuto oblast nazýváme prahová ekvivalentní dávka, odtud pravděpodobnost výskytu deterministických účinků s efektivní ekvivalentní dávkou roste, viz Obrázek 14. Samozřejmě i po účinné léčbě deterministických účinků a při ozáření dávkou menší než je prahová ekvivalentní dávka se mohou dostavit stochastické účinky.

Odezva lidského organismu na ozáření
14: Odezva lidského organismu na ozáření
P [%] pravděpodobnost deterministických účinků (nemoci z ozáření); H [Sv] efektivní ekvivalentní dávka. Toto je graf pro případ, že je ekvivalentní dávka rovnoměrně rozložená na celé tělo. Podrobnější popis například v [Hála, 1998, s. 145].

Stochastické účinky

Hirošima

Pro křivku pravděpodobnosti výskytu stochastických účinků chybí dostatečné množství dat, ale konzervativně se předpokládá jejich lineární růst z nuly. Například u osob, které přežily jaderný výbuch v Hirošimě byl po dobu 25 let od výbuchu zvýšený výskyt leukémie o 0,57 případů na 1 milion obyvatel na každou 10 mSv získanou ekvivlatení dávku oproti přírodnímu pozadí [Hála, 1998, s. 150], kdy přirozeně onemocní leukemií 1720 osob z 1 milionu. Pro představu v ČR je přirozená denní efektivní dávka 9-10 μSv (3,2 mSv/rok), rentgen zubů max 5 μSv, ale irigoskopie (vpíchnutí radioaktivní látky) až 7 mSv a CT vyšetření až 10 mSv. Umělé zdroje (včetně jaderných zařízení) přispívají ročně jen zcela minimálně asi 0,01 mSv.

 Kapitola: Účinky ionizujícího záření na lidský organismus
23.15

Tkáňový váhový faktor

Ekvivalentní dávka

Jestliže všechny tkáně obdržely stejnou dávku, tak se jednotlivé tkáně na deterministických účincích podílejí různou vahou. Například ve 12 % případech onemocní žaludek a jen v 1 % onemocní kůže při stejné obdržené dávce atp. Tyto statistické hodnoty pro jednotlivé tkáně lidského těla se označují jako tkáňový váhový faktor a jejich součet musí být 100 %, viz Tabulka 15. To znamená, že v případě, že obdržená dávka je po těle rozvržena nerovnoměrně je nutné vypočítat ekvivalentní dávky pro každý orgán zvlášť a ty sečíst viz Vzorce 12b a výsledkem je efektivní ekvivalentní dávka. Přičemž tentokrát je nutné hodnoty součinu DR·wR vynásobit tkáňovým váhovým faktorem dané tkáně.

tkáň, orgán   wT tkáň, orgán   wT tkáň, orgán   wT
červená kostní dřeň   0,12 gonády   0,08 povrch kostí   0,01
tlusté střevo   0,12 močový měchýř   0,04 mozek   0,01
plíce   0,12 jícen   0,04 slinné žlázy   0,01
žaludek   0,12 játra   0,04 kůže   0,01
mléčná žláza   0,12 štítná žláza   0,04 zbytek tkání   0,12
    ∑   1
15: Tkáňové váhové faktory podle ICRP 103
wT [-] tkáňový váhový faktor daného orgánu (Tissue weighting factor). ICRP–International commission on radiological protection. Zbytek tkání představuje: nadledvinky, horní cesty dýchací (Extrathoracic Region – ET), žlučník, srdce, ledviny, lymfatické uzliny, svalstvo, sliznice dutiny ústní, slinivka, prostata, tenké střevo, slezina, brzlík, děloha/hrdlo. [Valentin et al., 2007, s. 65]

Biologické účinky

Stochastické účinky

Ionizační záření může působit na úrovni buněk, sloučenin a atomů v lidském těle. Ve výsledku záření způsobí smrt buňky, nebo výrazně změny jejího chování změnou její molekuly DNA (mutace DNA), případně způsobí jiné poškození, které je buňka schopan opravit. Odúmíraní buněk je přirozený proces a tělo se jich dokáže zbavit a většinu nahradit při regeneraci pomocí kmenových buněk. Buňky, které změní svoji DNA natolik, že jsou rozpoznány imunitním sytémem za cízí objekty, jsou tímto systémem zničeny. Nejvíce nebezpečné jsou buňky s malými změnami DNA, které nemůže imunitní systém označit jako cizí tělesa, přestože jejich mutace DNA může vést na jejich chybné chování (mohou vytvářet i toxiny) a méně často k nekontrolovatelnému bujení, neboli k rakovině. Přičemž stochastické účinky mají pravděpodobně původ na počátku nevýznamným poškození DNA některých buněk, které se může zhoršit náhodným zachycením ionizujících částic z přírodního pozadí.

 Kapitola: Účinky ionizujícího záření na lidský organismus
23.16

Regenerace

Schopnost regenerace prakticky znamená, že při určité dávce je poškození organismu menší, je-li dávka buď rozprostřena rovnoměrně na delší dobu, nebo rozdělena na několik menších dávek s časovými prodlevami mezi nimi (frakcionace dávky), tak aby zasažená tkáň regenerovala rychleji než odumírala. Zpravidla platí, že buňky, které se nedělí (nerozmnožují) nebo se dělí pomalu jsou odolnější, než buňky, které se dělí rychleji (vlasy) – přesněji pravděpodobnost, že se mutace rozšíří je u buněk s nižší frekvencí dělení menší.

Na druhou stranu ionizující záření je naprosto nezbytné pro některé děje probíhající v biologickém cyklu zejména fotosyntézu. Fotosyntéza probíhá pomocí fotonů viditelného světla, kdy je zachcená energie využita k přetvoření organických sloučenin na molekuly glukózy.

Nemoc z ozáření

Při ekvivalentní dávce 1 až 2 Sv nastává akutní nemoc z ozáření (závisí na individuální odolnosti). Následuje několik fází onemocnění (nevolnost, skleslost, bolesti hlavy, zvracení a různé závažné změny v krevním obrazu podle stupně ozáření). Poté následuje latence a poté padání vlasů, silná vnímavost vůči infekcím. Při ozáření ekvivalentní dávkou 6 Sv převládá hematologická (hematologické změny tj. změny v krvetvorbě jsou popsány v [Garlík, 2012, s. 691]) forma nemoci pravděpodobnost přežití 20 %, při 10 Sv pravděpodobnost přežití se blíží k 0 %. Ozáření ekvivalentní dávkou 50 Sv způsobuje nervovou formu nemoci projevující se psychickou dezorientací a zmateností, křečemi a bezvědomím. Během několika hodin až dnů nastává smrt v důsledku oběhového kolapsu, zástavy dýchání a poruch mozku.

Léčebné účinky

Ozařování

Radiační onkologie

I když má ionizující záření na organismus (lidský) negativní vliv, tak ho lze využít k ničení nádorových buněk, čímž se zabývá obor zvaný radiační onkologie. Princip léčby je založen přibližně na 4 různých principech účinků ionizujícího záření na tkáně a popsané jsou v [Hála, 1998, s. 152]. Nejrozšířenější je léčba založena na plošném ozařování tkáně a předpokladu, že nádorové buňky se množí rychleji než buňky zdravé tkáně a tudíž jsou citlivější na ozařování a současně původní tkáň má schopnost regenerace.

 Kapitola: Účinky ionizujícího záření na lidský organismus
23.17

Protonová léčba

Druhý nejrozšířenější způsob se používá u pomalu rostoucích nádorů spočívá ve využití faktu, že protonová částice předává tkáni energii postupně (odrazy) podle Braggovy křivky (Obrázek 9), přičemž většinu energie předá pouze v oblasti vrcholu křivky. To znamená, že v případě lokálního nádoru lze většinu energie soustředit jen na něj a tkáň za ním nebude vůbec ozářena a před ním daleko méně než při plošném ozařování buněk. Parametry Braggovy křivky lze navíc měnit podle potřeby pomocí počáteční energie protonu, kterou je možno měnit v urychlovači díky tomu, že je to nabitá částice. Například při 180 MeV je dosah (konec křivky) ve tkání 15 cm [Hála, 1998, s. 154].

Úlohy

Úloha 1:
Alexandr Litviněnko zemřel na následky ozáření v roce 2006 poté co spolknul přibližně 10 μg radioaktivního polonia (izotop 210) [Gray, 2012, s. 195]. Vypočítejte: (a) jakou efektivní ekvivalentní dávku by obdrželo lidské tělo za 24 h po spolknutí čistého polonia (uvažujte izotop 210) – vyhodnoťte dopady při rovnoměrném zasažení celého organismu; (b) aktivitu pro případ čistého polonia a pro případ, kdy uplyne doba od výroby jeden rok. Za hmotnost těla dosaďte svou vlastní hmotnost. Řešení úlohy je uvedeno v Příloze 1.
1:   zadání:   τ; mPo; mT; t1; t2   odečet:   T1/2
2:   odečet:   wRα; wRγ   výpočet:   M; n; R0; λ; ΔR; εα; εγ; Dα; Dγ; HT
3:   odečet:   Eα; Eγ 4:   odečet:   τ
  odečet:   NA; mu; Ar   výpočet:   Rrok; A+rok; A+0
Popisek symbolů je v Příloze 1.
Úloha 2:
Muži o hmotnosti 85 kg byl nitrožilně aplikován jaderný izomer technecium 99mTc za účelem vyšetření kostí. Samotné vyšetření kamerou zachytávající gama záření proběhlo za 2 hodiny po aplikaci. (a) Vypočítejte aktivitu v okamžiku vyšetření, jestliže v okamžiku aplikace byla aktivita obdrženého technecia 803 MBq. (b) Vypočítejte podíl předané energie gama záření tělu, jestliže během působení technécia obdržel tento muž efektivní ekvivalentní dávku o hodnotě přibližně 4,6 mSv. (c) Navrhněte hodnotu fluence této události. (d) Diskutejte vliv tohot vyšetření na stochastické účinky vzniku leukemie u tohoto pacienta? Přičemž vycházejte z toho, že jádro 99mTc se deexcituje na radioizotop 99Tc s poločasem přeměny 6,0058 hodin, samotný radioizotop 99Tc má poločas přeměny 2,111×105 let. Řešení úlohy je uvedeno v Příloze 2.
§1   zadání:   m; τ; A+0; H; T1/2   výpočet:   ε; ΔR; E; ε/E
§2   výpočet:   λ; R0; ΔR; R; A+ §4   odečet:   ρ
§3   odečet:   Eγ; τ   výpočet:   r; V; Φ
Popisek symbolů je v Příloze 2.
 Kapitola: Odkazy
23.18

Odkazy

ŠKORPÍK, Jiří, 2024, Jaderná energie a technologie pro její využití , Transformační technologie, Brno, ISSN 1804-8293, https://www.transformacni-technologie.cz/jaderna-energie-a-technologie-pro-jeji-vyuziti.html.
ATKINS, P. W., 2005, Periodické království: cesta do země chemických prvků, Academia, Praha, ISBN 80-200-1185-4.
BĚHOUNEK, František, 1945, Svět nejmenších rozměrů, Jaroslav Tožička, Praha.
GARLÍK, Bohumír, 2012, Energie elektromagnetického pole, inteligentní budovy a lidský organismus, Energetika, 62(12), ČSZE, Praha, ISSN 0375–8842.
GONZALEZ, F. M., et al., 2021, Improved Neutron Lifetime Measurement with UCNτ, Phys. Rev., 127(16), DOI: 10.1103/PhysRevLett.127.162501.
GRAY, Theodore W., 2012, Prvky: obrazový průvodce všemi známými atomy ve vesmíru, Slovart, Praha, ISBN 978-80-7391-544-5.
HÁLA, Jiří, 1998, Radioaktivita, ionizující záření, jaderná energie, KONVOJ, Brno, ISBN 80-85615-56-8.
NĚSTĚRENKO, G., SOBOLEV, A., SUŠKOV, J., 1959, Atomová letadla, Naše vojsko, Praha. Z ruského originálu Primeněnije atomonych dvigatělej v avijaciji.
VALENTIN, J., as editor, 2007, The 2007 Recommendations of the International Commission on Radiological Protection, ICRP, Ottawa, ISBN 978-0-7020-3048-2. Vyšlo v českém překladu: Doporučení Mezinárodní komise radiologické ochrany 2007.
VOHLÍDAL, Jiří, JULÁK, Alois, ŠTULÍK, Karel, 1999, Chemické a analytické tabulky, Grada, Praha, ISBN 978-80-7169-855-5.
©Jiří Škorpík, LICENCE

Doplňkový mediální obsah