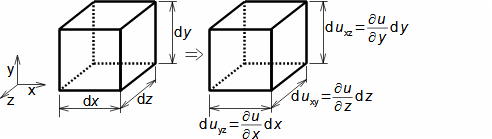
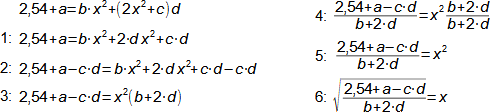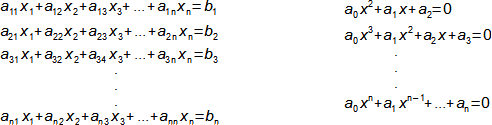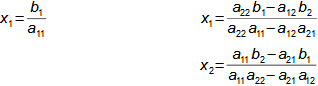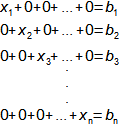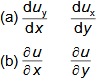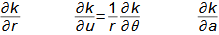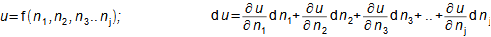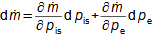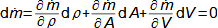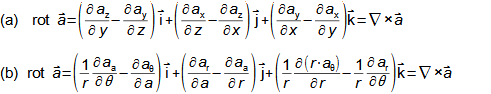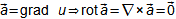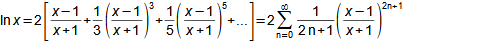Technická matematika

Škorpík, Jiří

TECHNICKÁ MATEMATIKA

1.3

Proč rozumět matematice a kdy toho využít v běžné technické praxi

Aktivní znalost matematiky

Může se zdát, že v běžné technické praxi v současném digitálním věku a masového používaní vypočetní techniky jako by vymizela potřeba aktivní znalosti matematiky, respektive znalosti matematických vzorců a metod. Vývoj softwaru pokročil tak daleko, že stačí vědět "co", ale nikoliv už "jak". Byla ta několikaletá výuka matematiky vůbce k něčemu? Využiji to někdy? Na tyto otázky se pokusím v této kapitole odpovědět.

Matematika

Zadání

Výsledek

Balistický počítač

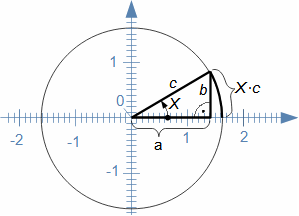
Podobnost

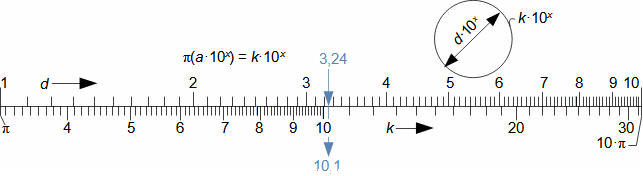
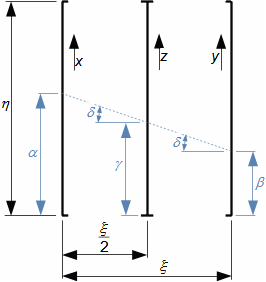
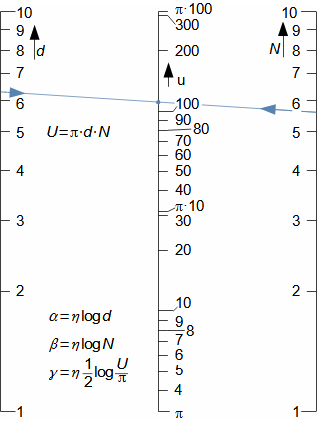
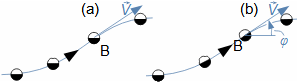
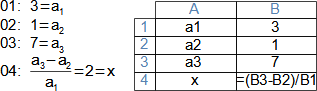
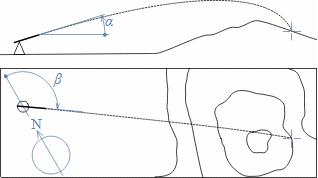
Matematiku v běžné technické praxi používáme jako abstraktního nástroje pro zpracování informací (zadání) za účelem jejich uspořádání podle požadovaných pravidel, ale častěji je nástrojem pro zpracování zadaných informací takovým způsobem, abychom získali konkrétní speciální informaci, kterou z prostých zadaných informací nelze lidskými smysly na první pohled vyčíst, nicméně ji nutně potřebujeme ke splnění nějakého úkolu. Běžně se tato speciální informace nazývá výsledkem. Příkladem vztahu zadání a výsledku je výpočet náměru a odměru děla pomocí balistického počítače tohoto děla. Zadáním v tomto případě je poloha děla, poloha cíle, parametry vzduchu, stav počasí, stav děla (počet výstřelů, teplota...), parametry náboje atd. Výsledkem jsou prakticky jen dvě čísla pro náměr a odměr (Obrázek 1), z nichž zadané parametry nelze zpětně odvodit. Současně ze zadání nelze prostými smysly náměr a odměr přesně stanovit, pouze zkušená obsluha by na základě podobnosti s předchozími výstřely byla schopna náměr a odměr prostými smysly odhadnout.

α [°] náměr; β [°] odměr.

Postup

Zadání

Výsledek

Při matematickém postupu zpracování zadání nevznikají žádné nové informace, což znamená, že matematiky je v jistém smyslu jakýsi převodník zadaných informací do požadované "užitečné" podoby [Gecsei et al., 1964, s. 21], [Mareš, 2006, s. 42]. To znamená, že už v samotné zadání je výsledek skryt. A zde je první jsou první změny, které přináší digitální věk při zpracování zadání do podoby výsledku. Při zpracování zadání

TECHNICKÁ MATEMATIKA

1.4

postupoval výpočtář iteračně, tj. postupně objevoval cesty pro výpočet a i dodatečně stanovoval údaje, kterými bylo nutné doplnit zadání, aby získal požadovaný výsledek. V digitálním věku se zadání pro technika stává nejdůležitější složkou jeho práce, respektive už úplně na záčátku musí mít velice podrobné zadání, aby se dostal ke správnému výsledku. A toho nedosáhne pokud nebu znát co je za digitálním výpočtem skryto za postup. Není nic nového na konstatování, že kvalita výsldku odpovídá kvalitě zadání, právě v tom se budou lišit výsledky výpočtářů, kteří rozumějí matematice od těch, které ji nerozumějí. Nicméně, po studiu matematiky díky přístupnosti výkonných výpočtových programů již "matematické převody" manuálně používat nebudete. Běžní inženýrské praxi lze opatrně podotknout, že je tedy důležitější vědět co než jak– s tím, že vědět co znamená, i to, že to řešitelné je.

Představivost

Studium

Pro inženýra je typické, že je schopen si pod rovnicemi něco konkrétního představit a to co si lze představit na to lze odpovědět přímo, bez složitého abstraktního počítání [Gowers, 2006]. Platí to i obráceně studium matematiky zvyšuje schopnost představovat si i velmi složité procesy. Matematika je také hlavní prostředek při studiu technických oborů, bez které by nebylo možné vysvětlit přírodní zákonitosti, ze kterých inženýr vychází při návrhu a realizaci svých děl.

Rychlé a přibližné výpočty

Kontrolní výpočet

Enrico Fermi

Děj

Rychlé přibližné výpočty se dělají obvykle bez elektroniky. Například pomocí počítání z paměti, pomocí tužky a papíru nebo pomocí předem připravených jiných výpočetních pomůcek. Především kontrolní výpočty je dobré provádět jiným nástrojem než byl proveden kontrolovaný výpočet, kvůli tzv. "autorské slepotě" a opakovaným překlepům s tím, že postačuje zkontrolovat, jestli se přibližný výsledek blíží přesnému výpočtu. Rychlé výpočty technici ocení také při práci v terénu pro získání rychlé orientace v problému. Občas už i přibližný výpočet umožňuje realizaci konkrétního díla a dostatečnou predikci jeho vlastností. Ostatně přibližné řádově přesné výpočty jako nástroj k pochopení děje prosazoval v USA už Enrico Fermi [Miodownik, 2016, s. 183]. To se potvrdilo i při vývoji atomových bomb, kdy někteří vědci byly schopni dělat velmi přesné předpovědi výsledků numerických výpočtů, které trvaly i několik měsíců, ale přitom bylo potřeba učinit závažné rozhodnutí hned [Jungk, 1965, s. 230].

Stres

Výpadek

Převodní pravítka

Nomogramy

Aktivní znalosti matematiky jsou nezbytnou součástí těch profesí, při kterých jsou sice využívány počítače, ale v případě jejich výpadku je ohrožena bezpečnost lidí nebo újmy na majetku. Takové situace navíc bývají obvykle současně dosti

TECHNICKÁ MATEMATIKA

1.5

stresující, takže je nutné být pro tyto situace speciálně školen včetně školení v použití jednoduchých výpočetních pomůcek, jako kalkulačky a převodníková pravítka či nomogramy. Například v případě výpadku balistického počítače výše musí obsluha, pomocí jednoduchých předem připravených pravítek a nomogramů, provést alespoň přibližné výpočty.

Na obrázku je Sally Ride (první Američanka ve vesmíru) na palubě raketoplánu Challenger. Všimněte si prosím záložních kalkulaček HP-41C pro případ výpadku počítačů. pic.twitter.com/br7114XPCJ
— Jiří Škorpík (@jiri_skorpik) July 4, 2023

Technická matematika

Článek Technická matematika není souhrn matematických metod a důkazů jejich platnosti, ale spíše se zaměřuji na konkrétní nástroje pro kontrolní a rychlé výpočty a technickou interpretaci matematických vzroců a metod včetně uvedení příkladů. Také se omezuji pouze na to, že technické úlohy v prostoru mají pouze tři rozměry a při nestacionárních úlohách je čtvrtým rozměrem čas.

Jak lze počítáním objevit nová čísla

Pouze skrz pochopení toho co jednotlivá čísla vyjadřují, lze správně interpretovat výsledky a pochopit vztah mezi geometrií a algebrou neboli analytickou geometrii, jejíž pochopení je pro technika naprosto klíčové.

Přirozená čísla

Základním stavebním kamenem čísel jsou přirozená čísla jako 1, 2, 3, 4..., které mají přímou souvislost s fyzickým světem při označovaní množství (tři jablka, sedm dnů...). Až používáním matematických operacích (sčítání, odčítání, násobení, dělení) s přirozenými čísly byla objevena čísla další, nejprve jako mezivýsledky a později našla uplatnění i jako konečné výsledky.

Záporná čísla

Při odčítání předešlých typů čísel byla objevena čísla záporná (nejprve používaná pouze jako mezivýsledky) například 2-4=-2. A proto musela vzniknout pravidla, jak s takovými čísly počítat, například bylo zavedeno, že násobením dvou záporných čísel vyjde číslo kladné, to je jedno z pravidel aritmetiky. Kdyby tomu tak nebylo a pravidlo by znělo například tak, že násobením dvou záporných čísel vyjde číslo záporné, musela by být aritmetická pravidla zvlášť pro kladná a záporná čísla [Stewart, 2013, s. 45] – prostě by počítaní také šlo, ale bylo by to složitější.

Racionální čísla

Přímou souvislost s fyzickým světem mají i čísla racionální. Jedná se o čísla vzniklá podílem dvou přirozených čísel (například polovina jablka 1/2=0,5). Výsledkem operace dělení nemusí být, a často ani nebývá, celé číslo, ale číslo desetinné, přičemž před i za desetinou čárkou může být libovolný ale konečný počet čísel.

Iracionální čísla

Na první pohled se zdá, že jakékoliv přirozené číslo lze dělit nekonečným počtem jiných přirozených čísel, a tak by bylo možné vyjádřit jakékoliv desetinné číslo, leč není tomu tak. Lze

TECHNICKÁ MATEMATIKA

1.6

celkem jednoduše dokázat, že například číslo √2= 2,4142... nelze vyjádřit podílem dvou přirozených čísel (jednoduché důkazy, že toto číslo nelze vyjádřit jako zlomek přirozených čísel jsou uvedeny v knihách Jazyk matematiky a Matematické důkazy [Devlin, 2003, s. 31] a [Thiele, 1985, s. 113]). Čísla, která nelze takovým podílem vyjádřit se nazývají iracionální čísla.

Reálná čísla

Nula

Představené typy čísel (přirozená, záporná, iracionální, racionální) jsou souhrnně nazývána jako čísla reálná, a hranice mezi kladnými a zápornými čísly je nula – při počítání má význam jako nic [Mazur, 2017, s. 92], prázdno apod. a není to reálné číslo (proto násobení nulou je nula a dělení nulou je nesmysl [Robinson, 2008, s. 39]). Někdy se uvádí při dělení nulou jako výsledek nekonečno (znak ∞), ale to jen ve speciálních případech, protože obrácená operace dělení je násobení a při násobení nekonečna nulou je výsledek opět nula a ne původní dělenec, více v knize Kabinet matematických kuriozit profesora Stewarta [Stewart, 2013, s. 93].

Osa reálných čísel

Reálná čísla a nulu lze znázornit i graficky pomocí osy, na které jsou seřazena čísla vzestupně zleva doprava, přičemž vzdálenosti mezi nimi jsou stejné, podle toho jak rozměrově velkou osu chceme vytvořit, viz Obrázek 2.

Množství vyznačených stupnic mezi dvěma přirozenými čísly označující dekadická racionální čísla 1/10, 1/100... (zde vyznačena pouze 1/10) je dána pouze rozlišením, tj. vzdáleností přirozených čísel. Iracionální a některá racionální čísla nelze na ose reálných čísel nikdy přesně zakreslit (mohou mít nekonečně mnoho desetinných míst), pouze lze jejich polohu zpřesňovat vyčíslením jejich velikosti na co nejvíce desetinných míst. Šipka na pravé straně označuje směr růstu kladných čísel.

Imaginární jednotka

Gaussova rovina

Leonhard Euler

Komplexní číslo

Matematický dvojčlen

Postupem času se začaly objevovat ve výsledcích matematický dvojčlen ve tvaru a+-b√(-1). √(-1) není to samé jako √1, protože 1² i -1² je 1. Nula to být nemůže, ta je jen jedna a znamená nic. Současně se jedná o jedno číslo, o kterém nevíme mezi jakými dvěma čísly by se mohlo na reálné ose čísel nacházet. To znamená, že když toto neidentifikovatelné číslo vynásobíme nebo k němu další číslo přičteme, tak stále výsledek nemůže ležet na reálné ose. Takže se jedná o nové číslo, které neleží na ose reálných čísel a pro lepší představivost jsme kvůli němu začali používat zcela nový systém os, abychom je mohli zapisovat, který nazýváme Gaussovou rovinnou, viz níže.

TECHNICKÁ MATEMATIKA

1.7

Současně byl zaveden Leonhardem Eulerem pojem imaginární jednotka i [Devlin, 2003, s. 138], která je krátkým symbolem pro výraz √(-1), takže uvedený matematický dvojčlen by šel zapsat ve tvaru a±i·b a nazýváme ho komplexním číslem. S komplexním číslem se pracuje jako s matematickým dvojčlenem akorát dělení je trochu složitější [Rektorys et al., 2003, s. 9] a je potřeba si dát pozor i na součin i·i, který nemůže být roven 1, protože to už je reálné číslo. Komplexní číslo je čistě abstraktní veličina – je to produkt matematických pravidel.

Komplexní číslo ve výpočtech

Výsledky ve tvaru komplexních čísel se poprvé začaly objevovat při řešení kvadratických rovnic a později i jako řešení diferenciálních rovnic. Takový výsledek se dá interpretovat více způsoby (pokud se nejedná o mezivýsledek, se kterým se dále pracuje). Vždy záleží na spojitosti s výpočtem, respektive co je vlastně počítáno.

Gaussova rovina

Gaussova rovina je tvořena dvěma vzájemně kolmými osami, proto ji také nazýváme i rovinou komplexních čísel. Na vodorovnou vynášíme hodnoty a, která má stejné vlastnosti jako osa reálných čísel – obsahuje i nulu. Nulou prochází osa čísel b, která má také vlastnosti osy reálných čísel a je kolmá k ose čísel a. Komplexní čísla se v takovém systému zakreslují tak, jak je znázorněno na Obrázku 3.

Bod P je komplexní číslo 2-i·1,4 znázorněné v Gaussově rovině.

Při práci v rovině se v odborné literatuře velmi často používá algebra komplexních čísel (kde osa x je osou parametrů b a osa y osou parametrů a komplexního čísla), která defacto popisuje operace v rovině – zdůrazňuji, že se využívá pouze algebra, takže ve skutečnosti se nejedná o práci s komplexními čísly, ale čísly reálnými. Komplexní číslo většinou není v technické praxi

TECHNICKÁ MATEMATIKA

1.8

přijatelný výsledek a musí se umět správně interpretovat co by to mohlo znamenat pro postup výpočtu nebo popisovaný děj.

Kvaterniony a oktoniony

Mimo zmíněná čísla existují ještě čísla nazývaná kvaterniony a oktoniony [MAREŠ, 2008], ale ty se v běžné technické praxi už nevyskytují.

Zaokrouhlování

Pravidla zaokrouhlování

Mezi základní problémy rychlých a přibližných výpočtů patří zaokrouhlování. V současné době díky počítačům není problém pracovat s čísly, které mají velký počet desetinných míst. Taková čísla jsou matematicky sice velmi přesná, ale v běžných technických případech těžko využitelná, zvláště pro přibližné a rychlé výpočty je lepší taková čísla zaokrouhlovat (zkracovaní čísla). Tři základní matematická pravidla zaokrouhlování, která jistě znáte, se dají shrnout do těchto tří příkladů: 4,335≐4,34≐4,3, ale pokud se jedná o desetinné číslo končící číslicí 5 s následujícími nulami zaokrouhluje se obvykle na nejbližší sudé číslo: 4,38500≐4,38, 4,37500≐4,38 [Dobrovolný and Žďárek, 1954, s. 32]. Tzn. poslední dvojciferné číslo končící číslem 4 a menším se zaokrouhluje směrem dolů, poslední dvojciferné číslo končící číslem 6 a vyšším se zaokrouhluje směrem nahoru.

Dvouciferné zaokrouhlování

Pro rychlé přibližné výpočty se čísla zaokrouhlují obvykle pouze na dvouciferné desetinné místo například: 4335≐4,3·10³, 0,004335≐4,3·10^-3.

Zaokrouhlování v technice

Zaokrouhlováním se dopouštíme jisté chyby. O teorii chyb bylo napsáno spousta knih, ale pro přibližné výpočty v technické praxi lze doporučit jedno "lidové" pravidlo a to zaokrouhlovat na stranu bezpečnou. To znamená, že počítáme-li přibližně nosnost nějaké konstrukce, tak zaokrouhlujeme čísla dolů. Konečný výsledek sice bude nepřesný, ale s vědomím, že skutečná nosnost bude vyšší a ne nižší. Naopak budeme-li počítat velikost zatěžující síly, tak zaokrouhlováním vždy nahoru bude výsledek nepřesný, ale s vědomím, že skutečná zatěžující síla bude menší apod.

Jednoduché ruční výpočty pomocí tužky a papíru

Počítání "pod sebou"

Sčítání a odčítání

Pokud chceme počítat bez kalkulačky či počítače s většími čísly, pak obvykle přistupujeme k počítání "pod sebou" pomocí tužky a papíru . Tzv. sčítání, odčítání pod sebou souvisí se zavedením pozičního systému zápisu arabských čísel [MAREŠ, 2008], [Struik, 1963], který se do západní Evropy dostal pomocí

TECHNICKÁ MATEMATIKA

1.9

Muhamad ibn Músa al-Chwárizmí

spisů perského učence Muhamad ibn Músa al-Chwárizmí (780-850) [MAREŠ, 2008], [Struik, 1963]. V takovém případě stačí napsat čísla pod sebe a jednotlivé řády k sobě přičítat, respektive odčítat. Připomenutí takového postupu je na Obrázku 4.

Při odčítání většího čísla od menšího je praktičtější jejich pozice přehodit a rozdíl doplnit znaménkem -.

Násobení a dělení

Operace násobení a dělení jsou obtížnější, co se týká výpočtů z hlavy. Podobně jako pro sčítání a odčítání tak i pro násobení a dělení lze provádět metodou "počítáním pod sebe". Při násobení se násobená čísla napíši pod sebe podle řádů jako u sčítání a postupně se vzájemně násobí jednotlivé řády činitelů, tyto násobky se na konci sečtou. Při dělení se hledají násobky dělitele, který se postupně odečítá od dělence. Připomenutí takového postupu je na Obrázku 5.

Konstrukce pravítek a nomogramů pro výpočety vzorců

Sčítání a odečítání pomocí pravítka

Přesnost

Rychlé zaokrouhlené sčítání a odčítání lze provádět pomocí analogových pomůcek jako je posuvné pravítko pro sčítání a odčítání. Posuvné pravítko je složeno ze dvou identických posuvných lišt s číselnou osou, kde jednotlivé stupnice musí být od sebe stejně vzdálené (vlastně se jedná o dvě osy reálných čísel). Takové pravítko lze vytvořit například ze dvou stejných pravítek pro rýsování. Jestliže chceme znát hodnotu a+b, pak první pravítko posuneme tak, aby ryska odpovídající nule měla naproti rysku odpovídající hodnotě a, výsledek pak odpovídá rysce na druhém pravítku, která ma naproti rysku prvního pravítka s hodnotou b. Vzhledem k omezení viditelnosti stupnice by pravítko o délce 20 centimetrů se stupnicí po 0,5 mm bylo schopno přičítat nebo odčítat čísla od 1 do 10 s přesností na 0,05 a pod.

Převodník aditivních jednotek

Takové pravítko, zvyšuje přesnost oproti přibližnému výpočtu "z hlavy" málo a nemá praktický smysl ho používat. Ale používá se jako převodník jednotek, přesněji pro převod mezi

TECHNICKÁ MATEMATIKA

1.10

Absolutní teplota

Atmosférický tlak

dvěma různými jednotkami stejné veličiny, které se od sebe liší pouze o nějakou přičtenou číselnou hodnotu. Například k naměřené teplotě ve stupních Celsia se musí přičíst teplota absolutní nuly (273,15 °C), pro získání teploty absolutní (Obrázek 6). Další podobný případ je práce s absolutním tlakem, kdy k odečtenému tlaku z manometru se musí přičíst tlak atmosférický (101,325 kPa), pro získání tlaku absolutního, viz Obrázek 7 (samozřejmě pro tlaky řádu desítek MPa už stačí připočítat jen jednu desetinu a převodník ztrácí smysl).

Příklad pravítka pro součet/rozdíl stále stejného čísla

Převodník jednotek teploty v rozsahu 0 až 100 °C na absolutní teplotu v Kelvinech a obráceně: Na obrázku je vyznačen případ, kdy teploměr ukazuje 56 °C, pomocí narýsovaného pravítka velmi rychle vypočítáme, že tato teplota odpovídá 329,15 K.

Převodník přetlaku v rozsahu 0 až 100 kPa(g) na absolutní tlak a obráceně: Znak (a) v závorce označuje absolutní tlak, znak (g) označuje přetlak (ang. naměřený).

Stresová situace

S podobnými jednoduchými převodníky se můžeme setkat především v místech, kde mohou nastat stresující situace, kdy obsluha zařízení nemusí být schopna ani jednoduchých matematických úkonů.

Násobení a dělení pomocí pravítka

Logaritmické pravítko

Složitější matematické operace jako je násobení a dělení lze provádět pomocí logaritmického pravítka založené na vlastnostech logaritmů, proto si nejprve řekněme něco o logaritmech. Každopádně Objev logaritmů měl na vědu dopad srovnatelný s vynálezem počítače [Tesařík, 2015].

Logaritmus čísla

Logaritmy jsou založeny na faktu, že každé kladné reálné číslo x lze vyjádřit umocňováním ve tvaru x=n^y (záporná reálná čísla lze vyjádřit umocňováním pomocí algebry komplexních čísel). Logaritmus čísla je tak definován jako log_n n^y=y·log_n n=y·1, kde n je základ umocňování, respektive logaritmu a log_n n=1.

TECHNICKÁ MATEMATIKA

1.11

Dekadický logaritmus

Přirozený logaritmus

Eulerovo číslo

Nejčastěji se používají tzv. dekadické logaritmy, což je logaritmus o základu 10, a proto se zkráceně označují pouze log. Přirozený logaritmus se označuje ln (dříve lg), ten je o základu e=2,71828... (tzv. Eulerovo číslo, které souvisí s nekonečnými řadami). V počtu pravděpodobnosti a informatice se také používá logaritmus o základu 2, tzn. log₂, který už speciální označení nemá. Logaritmy o různých základech lze převádět mezi sebou pomocí vztahu log_n x=(ln x)/(ln n). Log 0 je v matematice neurčitý výraz a pokud to lze definuje se jako 0·log 0=0 [Gecsei et al., 1964, s. 16].

Násobení a dělení pomocí dekadického logaritmu

Z vlastností logaritmů lze součin čísel a a b převést na součet dvou logaritmů takto: a·b=c => log a+log b=log c=C. Chceme-li zjistit hodnotu c. Pro výsledek c pak platí rovnost c=10^C. Podobný převod lze provést při dělení čísel a a b: a·b^-1=c => log a-log b=log c=C. Alegebra logaritmů je shrnuta v [Rektorys et al., 2003, s. 14].

Logaritmy čísel 1 až 100

x	log x	x	log x	x	log x	x	log x
1	0	26	1,4150	51	1,7076	76	1,8808
2	0,3010	27	1,4314	52	1,7160	77	1,8865
3	0,4771	28	1,4472	53	1,7243	78	1,8921
4	0,6021	29	1,4624	54	1,7324	79	1,8976
5	0,6990	30	1,4771	55	1,7404	80	1,9031
6	0,7782	31	1,4914	56	1,7482	81	1,9085
7	0,8451	32	1,5051	57	1,7559	82	1,9138
8	0,9031	33	1,5185	58	1,7634	83	1,9191
9	0,9542	34	1,5315	59	1,7709	84	1,9243
10	1	35	1,5441	60	1,7782	85	1,9294
11	1,0414	36	1,5563	61	1,7853	86	1,9345
12	1,0792	37	1,5682	62	1,7924	87	1,9395
13	1,1139	38	1,5798	63	1,7993	88	1,9445
14	1,1461	39	1,5911	64	1,8062	89	1,9494
15	1,1761	40	1,6021	65	1,8129	90	1,9542
16	1,2041	41	1,6128	66	1,8195	91	1,9590
17	1,2304	42	1,6232	67	1,8261	92	1,9638
18	1,2553	43	1,6335	68	1,8325	93	1,9685
19	1,2788	44	1,6435	69	1,8388	94	1,9731
20	1,3010	45	1,6532	70	1,8451	95	1,9777
21	1,3222	46	1,6628	71	1,8513	96	1,9823
22	1,3424	47	1,6721	72	1,8573	97	1,9868
23	1,3617	48	1,6812	73	1,8633	98	1,9912
24	1,3802	49	1,6902	74	1,8692	99	1,9956
25	1,3979	50	1,6990	75	1,8751	100	2

Příklad: Pro 4·8 musí platit log 4·8 = log 4 + log 8. Z tabulky log 4 = 0,6021; log 8 = 0,9031, odtud log 4·8 = 1,5052. Číslo 1,5052 je velice blízké číslu logaritmu čísla 32, takže můžeme tvrdit, že součin 4·8 bude velmi blízký číslu 32. Samozřejmě čím přesnější čísla v tabulce, tím lze očekávat přesnější výsledek.

TECHNICKÁ MATEMATIKA

1.12

Hodnoty logaritmů čísel

Taylorovy řady

Pro výpočty pomocí logaritmů je nutné znát hodnoty logaritmů. Ty se dříve tabelizovaly a první tabulky dekadických logaritmů publikoval Briggs (viz Tabulka 8). V té době vyčíslení logaritmů představoval pracný ruční výpočet přirozeného logaritmu a převodu na dekadický logaritmus. Současné matematické softwary a kalkulačky tyto tabulky obsahují nebo si je počítají v reálné čase numerickým způsobem na požadovanou přesnost pomocí Taylorových řad [Gecsei et al., 1964, s. 182].

Logaritmická stupnice

Všimněte si, že pokud hodnoty dekadických logaritmů vyneseme na osu (viz Obrázek 9) jsou hodnoty logaritmů jednotlivých řádů stejně vzdálené. To je dáno tím, že podíl mezi sousedními řády jsou stejné 10/1=100/10=1000/100... a tedy i rozdíl (vzdálenost) logaritmů sousedních řádů je stejný.

Porovnání lineární a logaritmické stupnice kladných reálných čísel

Horní osa je osa přirozených čísel od 1 do 10 o délce η=17 cm, takže jeden stupeň na stupnici je 1=1,7 mm, dolní osa je logaritmická stupnice od od 1 do 10 o délce ξ=17 cm. Jednotlivé vzdálenosti mezi stupni logaritmické stupnice v mm se vypočítají jako poměr konkrétní logaritmické hodnoty ku logaritmické hodnotě celé stupnice. Takže log x musí být ekvivalentní vzdálenosti ξ(log x – log min)/(log max – log min), v tomto případě log min =log 1=0, log max=log 10=1.

Logaritmické pravítko

Williamem Oughtredem

I když se tabulky logaritmů udávaly na pět i více desetinných míst, k výpočtům prostých součinů se nepoužívali, protože rychlejší bylo násobení pod sebou. Pro rychlé přibližné výpočty se používalo logaritmické pravítko vynalezené anglikánským duchovním a matematikem Williamem Oughtredem (1575-1660). Logaritmické pravítko funguje stejně jako posuvné pravítko pro sčítání a odčítaní s tím rozdílem, že obě stupnice odpovídají logaritmům čísel. Takže při násobení čísla 4,4 s číslem 6,3 stačí sečíst logaritmy těchto čísel na dvou zrcadlově otočených pravítkách s logaritmickou stupnicí (Obrázek 10). Při dělení se logaritmy odčítají.

TECHNICKÁ MATEMATIKA

1.13

10:

Příklad násobení pomocí logaritmického pravítka

Na obrázku je zobrazen případ přibližného součinu čísel 4346 a 6328, pomocí dvou pravítek se stupnicemi od 0 do 20 rozdělených po log 0,1. Přibližný součin je proveden tak, že činitelé se zaokrouhlí na 4400 a 6300, potom 4400·6300=4,4·6,3·10⁶, respektive log 4,4+log 6,3=log 27,8+log 10⁶. Podle pravítka je výsledek 27,8·10⁶, oproti přesnému výsledku je rozdíl 498 512, což odpovídá chybě 1,8 %.

Úloha 1:

Určete výsledek výrazu 14 468,56³ pomocí logaritmů. Řešení úlohy je uvedeno v Příloze 1.

Logaritmické převodníky

Výpočet obvodu kruhu

Výpočet plochy kruhu

Nicméně logaritmické pravítko je také už archaická pomůcka, ale narýsované pravítko, které by násobilo stále stejnou hodnotu lze použít jako rychlý převodník, například pro rychlý převod fyzikálních jednotek, které jsou vzájemným násobkem nebo i pro výpočet obvodu či plochy kruhu jak ukazují následující Obrázky 11, 12 a dále Obrázky 13, 14, 15, 16, 17.

Poslední logaritmické pravítko vyrobené ve Spojených státech bylo vyrobeno 11.července 1976, začala éra kapesních kalkulaček.https://t.co/dEBKKmJGp1 pic.twitter.com/1mgCU6S7Up
— kalendarbeda (@kalendarbeda) July 11, 2024

11:

Příklad logaritmického pravítka pro násobení nebo dělení konstantou

Logaritmické pravítko pro výpočet obvodu kruhu: Na pravítku je vyznačen příklad součinu čísla π a čísla 324 představující průměr kruhu, takže výsledkem bude obvod tohoto kruhu. Ten podle pravítka činí asi 1 010 (x=2), což představuje chybu od přesnějšího výsledku (1017,88) asi 0,77 %.

TECHNICKÁ MATEMATIKA

1.15

13:

Převodník palců na milimetry

14:

Převodník liber na kilogramy

15:

Převodníky jednotek energie

16:

Převodník výkonu Britského koně (horse-power) na watty

17:

Převodníky jednotek tlaku

TECHNICKÁ MATEMATIKA

1.16

Konstrukce logaritmického převodníku

Pro konstrukci logaritmických stupnic pro konstrukci vlastních převodníků o velikosti 10^x až 10^x+1 s přesností 0,1·10^x můžete použít logaritmy čísel 1 až 100 uvedené v Tabulce 8 nebo podrobněji ve starší literatuře jako třeba Fyzikálně technické příručce [Jakovlev et al., 1963].

Přesnost převodníků

Vyšší přesností výpočtu, pomocí zobrazeného logaritmického pravítka, lze provést rozkladem činitele. Například při výpočtu kruhu na Obrázku 11 by šlo postupovat přesněji takto: číslo 324 lze rozložit na 324=3·10²+2·10²+4, takže předchozí příklad by se počítal: π·324=π(3·10²+2·10²+4), odtud řešení 1015,4 s chybou už jen 0,24 %. Tento postup (více o něm například v knize Matematika pro dělníky a mistry [Kunc and Jozífek, 1963]) je sice přesnější, ale už postrádá rychlost a jednoduchost.

Nelogaritmické převodníky

Stupnice převodníků, ve kterých figurují násobky nemusí být nutně logaritmické, ale pokud rozdíly v převáděných jednotkách nejsou velké, lze použít lineární stupnice s tím, že budou mít rozdílné vzdálenosti mezi jedním stupněm. Například převodník mezi °C a stupni °F pro rozsah 0 až 100 °C a délce 17 cm bude mít na stupnici pro stupně Celsia vzdálenosti mezi stupni 1,7 mm, kdežto na stupnici stupňů Fahrenheita bude rozdíl jednoho stupně 5/9·1,7 = 0,9444 mm (stupeň Fahrenheita je 5/9 stupně Celsia), navíc bude tato stupnice vůči předchozí stupnici posunuta o 32 dílků, viz Obrázek 18.

18:

Převodník jednotek teploty v rozsahu 0 až 100 °C na teplotu ve stupních Fahrenheita a obráceně

Vzorec s více proměnnými

Nomogram

Pro výpočet vzorců s více proměnnými lze použít nomogramy. Nomogram je grafická analogová výpočetní pomůcka [Pleskot, 1947], [Štěpanský, 1970], [Evesham, 2010]. Jedná se o převod funkcí do grafické podoby ve vhodně vybraném soustavě souřadnic (nejčastěji pravoúhlé). Nomogramy vychází tedy z pravidel analytické geometrie v rovině [Devlin, 2003, s. 161], [Struik, 1963, s. 97], což jsou pravidla pro grafické vyjádření funkcí dvou proměnných. Nomogramy, na rozdíl od pravítek, umožňují rychlý výpočet rovnic více proměnných. Používají se pro rychlý přibližný výpočet často používaných vzorců.

TECHNICKÁ MATEMATIKA

1.17

Obvodová rychlost

Isopléta

Například nomogram pro výpočet obvodové rychlosti (U=π·d·N, kde U [m·s^-1] je symbol a značka jednotky obvodové rychlosti, d [m] je průměr kola a N [s^-1] jsou otáčky) kola je tvořen přímkami, protože pro konstantní průměr kola je tato rovnice rovnicí přímky – křivka konstantních hodnot funkce se nazývá isoplétou, viz Obrázek 19. Takový nomogram lze zkonstruovat pouze pravítkem. Nutné je stanovit rozsah jednotlivých proměnných podle toho, které kombinace hodnot d a N nás zajímají.

19:

Nomogram obvodé rychlosti

Nomogram pro výpočet obvodové rychlosti kola

U [m·s^-1]; d [m]; N [s^-1]. Osa otáček je v intervalu 1 až 10 s^-1, osa obvodové rychlosti kola 0 až 300 m·s^-1. Do oblasti řešení, která je vymezená vodorovnou osu hodnot pro otáčky a svislou pro obvodovou rychlost kola se zakreslují průběhy změn obvodové rychlosti v závislosti na otáčkách pro jednotlivé průměry kola (čára, na které je jedna z proměnných konstantní – v tomto případě průměr kola se nazývá isopléta). První isopléta byla nakreslena ze souřadnic U=3,1415 při N=1 do bodu U=31,415 při N=10. Následující isopléty byly nakresleny stejným postupem. Obvodová rychlost kola se odečte z průsečíku zadaných hodnot otáček a průměru kola.

Systém souřadnic nomogramů

Osy soustavy souřadnic nemusí být u nomogramů navzájem kolmé, ale mohou svírat i jiný úhel než 90°. V systému skloněných os se poměrově zvětší či zmenší úhly mezi isoplétami a osami nomogramu. Například pokud by osa x svírala s osou y úhel 70°, pak by se úhel mezi isoplétami a osami zmenšil poměrem 70/90 apod.

Problém přesnosti nomogramu

Je očividné, že takový nomogram pro funkci dvou proměnných nemůže pokrýt všechny možnosti řešení v navrženém intervalu vstupních proměnných, to by musel obsahovat nekonečný počet isoplét, a nikoliv jen deset. Jestliže nomogram neobsahuje isoplétu splňující zadání, je nutné její průběh určit alespoň přibližně tak, jak naznačuje příklad výpočtu obvodové rychlosti pro N=6,3 s^-1 a d=5,6 m. Další problém přesnosti nomogramů tkví v jeho fyzické velikosti. Rozsah chyby

TECHNICKÁ MATEMATIKA

1.18

(chyba, která vznikne na délce 1 mm osy nomogramu) lze jednoduše stanovit z měřítka nomogramu. Tato chyba nemusí být na celé ploše nomogramu stejná. Například v případě posledního nomogramu v oblasti kolem N=2, d=2 bude vzdálenost 1 mm na ose obvodových otáček kola představovat chybu o velikosti ~24 % a v oblasti N=9, d=10 chybě jen ~1 %.

Výhody nelineárních stupnic

Rozdíly v přesnosti lze vyřešit nelineárními stupnicemi os, tak aby chyba v odečtu byla přibližně stejná na celé ploše nomogramu. Typ nelineární stupnice osy závisí na druhu rovnice, kterou nomogram zobrazuje, přičemž každá osa může mít jinou stupnici. Pro exponenciální rovnice (včetně exponentu 1) se nejčastěji používá logaritmická stupnice, ale ve speciálních případech lze použít stupnici kvadratické (pro kvadratické rovnice) atd.

Výhody logaritmické stupnice

V případě logaritmické stupnice je její výhoda i v tom, že jakékoliv exponenciální rovnice se dají znázornit jako přímky, například rovnice a·b^3,4=c bude přímkou ve tvaru log a + 3,4·log b=log c apod. Nomogram pro výpočet obvodové rychlosti kola v logaritmických stupnicích je zobrazen na Obrázku 20.

20:

Nomogram pro výpočet obvodové rychlosti kola v logaritmické soustavě souřadnic

Velikost tohoto nomogramu je 8,35x8,35 cm, takže chyba 1 mm v oblasti N=2, d=2 je asi 6,6 % a v oblasti N=9, d=10 je také 6,6 %, přičemž přesnost lze zvýšit zvětšením velikosti plochy nomogramu a zvýšením hustoty stupnic. V logaritmické soustavě souřadnic tedy lze dosáhnout stejné přesnosti, respektive nepřesnosti na celé ploše nomogramu. Více o rozboru přesnosti v logaritmické soustavě souřadnic v [Pleskot, 1947, s. 12].

Speciální oblasti nomogramů

Viskozita

Do jednoho nomogramu lze zakreslit i více rovnic, které mají stejné proměnné. Například do nomogramu pro obvodovou rychlost kola lze zakreslit i průběh pro kritické otáčky hřídele s tímto kolem, které se s průměrem kola budou měnit (kritické otáčky jsou funkcí průměru kola a tuhosti hřídele, která je v tomto případě stejná). V nomogramu lze také vyznačit různé oblasti, respektive kombinace, které jsou preferovány, nebo naopak nevhodné, či vyznačují něčím jiné významné oblasti –

TECHNICKÁ MATEMATIKA

1.19

například v Nomogramu 21 pro výpočet Reynoldsova čísla. Takto lze nomogramy personalizovat podle toho jakou oblastí se vlastník nomogramu zabývá.

21:

Nomogram pro odečet Reynoldsových čísel: V‾ [m·s^-1] střední rychlost proudění; L [mm] charakteristický rozměr; ν [m²·s^-1] kinematická viskozita; Re [1] Reynoldsovo číslo. a-rozsah kinematických viskozit vody mezi 0 °C a 100 °C; b-rozsah kinematických viskozit suchého vzduchu mezi 0 °C a 100 °C. Re_C [1] rozsah kritických Reynoldsových čísel pro potrubí. Obrázek je převzat z článku Vnitřní tření tekutiny a vývoj mezní vrstvy [Škorpík, 2023a]

Uživatelské nomogramy

Nomogramy se také dodávají k různým výrobkům jako pomůcka pro koncového uživatele o změnách parametrů stroje při různých nastavení. Například nomogramy u soustruhů, pro odečet otáček nebo posuvu při změně převodového poměru, nomogramy regulačních ventilů, ze kterých lze vyčíst změnu průtoku a tlakové ztráty při změně zdvihu vřetena ventilu apod.

Sdružené nomogramy

Nomogram zvládne i více proměnných než jen dvě, takové nomogramy se nazývají sdružené. Jedná se vlastně o dva nomogramy, které mají jednu společnou stupnici, která slouží jako výstup prvního a vstup do druhého.

Průsečíkové nomogramy

Doposud popsané typy nomogramů se nazývají průsečíkové. Nevýhodou těchto nomogramů je obtížný odečet (hledání průsečíku tří různoběžných čar) i velká hustota čar, proto se koncovým uživatelům, kteří nejsou tak matematicky zdatní pokud to jde, dodávají graficky přehlednější spojnicové nomogramy.

Spojnicové nomogramy

Spojnicový nomogram pro dvě proměnné je složen ze tří stupnic, na kterých jsou v příslušných měřítkách vyneseny hodnoty jednotlivých proměnných, respektive hodnoty počítané veličiny, viz nejjednodušší tvar spojnicového nomogramu Obrázek 22 tvořeného třemi přímkami z nichž jedna je uprostřed.

TECHNICKÁ MATEMATIKA

1.20

Konstruktér nomogramu musí navrhnout typ stupnic a jejich měřítka, jejich tvar a sklon i jejich vzájemné vzdálenosti tak, aby průsečíky na jednotlivých osách, které vzniknout nakreslením libovolné přímky, byly řešením příslušné rovnice.

22:

V tomto případě musí být jedna z os přesně uprostřed dvou dalších, ale lze ji podle potřeby posouvat, pokud se změní měřítko jedné z hlavních os – osa z bude přesně uprostřed, jestliže hlavní osy budou ve stejných měřítkách. Tento tvar spojnicového nomogram je vhodný pro rovnice ve tvaru α+β=2 γ (odvození je v Příloze 15), například a·x+b·y=c·z, kde a, b, c jsou konstanty; například x²+y²=z², což je Pythagorova věta apod. Jestliže osy jsou logaritmické stupnice lze tento součtový spojnicový diagram také použít pro součin např. rovnici x·y=z, která bude mít v logaritmických souřadnicích tvar log x+log y=log z, což už je rovnice přímky.

Obvodová rychlost kola

Příklad konstrukce spojnicového nomogramu je opět proveden na rovnici pro výpočet obvodové rychlosti kola, viz Nomogram 23. Všimněte si, že kdyby osa obvodových otáček U nebyla uprostřed, ale například blíže k ose průměrů, pak by se

23:

Spojnicový nomogram pro výpočet obvodové rychlosti kola

Postup konstrukce tohoto spojnicového nomogramu je popsána v Příloze 16.

TECHNICKÁ MATEMATIKA

1.21

musela měřítka těchto os různě změnit (měřítko osy průměrů více než osy rychlostí) a naopak. Proto je výhodné mít osu z uprostřed os hlavních.

Kombinované nomogramy

Spojnicové nomogramy lze také konstruovat pro více jak tři proměnné spojením několika nomogramů tzv. sdružený spojnicový nomogram. Dokonce lze kombinovat průsečíkové nomogramy s nomogramy spojnicovými [Pleskot, 1947, s. 136], [Štěpanský, 1970, s. 215].

Podobnosti nomogramů

Konstrukce nomogramů často vyžadují většího duševního úsilí a zkušeností. Ten kdo nemá dostatek zkušeností může vycházet při konstrukci nomogramu z podobnosti s jiným nomogramem (například tvarem řešené rovnice), přičemž lze čerpat z katalogů nomogramů uvedených v [Pleskot, 1947], [Štěpanský, 1970], [Opava, 1972].

Zpracování naměřených dat v logaritmické soustavě souřadnic

Exponenciální funkce

Logaritmická soustava souřadnic

Tlaková ztráta potrubí

Při konstrukci nomogramů v logaritmické soustavě souřadnic využíváme ten fakt, že exponenciální funkce jsou přímkami. Tato vlastnost logaritmické soustavy souřadnic se využívá při zpracování dat, které byly získány při vyšetřování nějakého děje u něhož se předpokládá, že ho lze popsat nějakou exponenciální funkcí. Příklad takového využití je na Obrázku 24 je výsledek takové aplikace. Jedná se o úlohu, ve které je cílem

24:

Hodnoty naměřené tlakové ztráty v potrubí zakreslené na logaritmickém papíře

Určení exponenciální funkce popisující závislost tlakové ztráty na průtoku potrubím. Očekávaný tvar této funkce je L_p=C_S·Q^x. V první kroku byla zanesena naměřená dat do logaritmických souřadnic (modré křížky). V druhém kroku byly tyto body proloženy přímkou (b). Víme, že směrnice přímky v logaritmické soustavě souřadnic představuje hodnotu exponentu x, a jelikož je přímka (b) rovnoběžná s přímkou (a), která představuje exponenciální rovnici s exponentem 2, je očekávaná hodnota exponentu x 2. Hodnotu konstanty C_S lze pak určit z jakéhokoliv bodu na přímce (b), pro který odečteme hodnoty pro L_p a Q a následně dosadíme do rovnice. L_p [Pa] tlaková ztráta, [m³·s^-1] průtok; C_S [kg·m^-7] konstanta. Obrázek je převzat z článku Vznik tlakové ztráty při proudění tekutiny a její výpočet [Škorpík, 2023b].

TECHNICKÁ MATEMATIKA

1.22

určit tzv. charakteristiku potrubního systému, kterým protéká voda. Měřena je tlaková ztráta potrubí, označovaná jako L_p, v závislosti na objemovém průtoku Q tímto potrubím, přičemž cílem je sestavit rovnici, která by tyto změny tlakové ztráty při změně průtoku predikovala, tedy rovnici L_p=f(Q).

Logaritmický papír

Pro aproximaci naměřených dat přímkou v logaritmické soustavě souřadnic se využívá výpočetní technika, ale vedle výpočetní techniky lze použít i ruční přístup pomocí logaritmického papíru. Za tímto účelem je na Obrázku 25 zobrazen logaritmický papír o velikosti 17x17cm a v rozsahu tří řádů.

25:

TECHNICKÁ MATEMATIKA

1.23

Sestavení rovnic ze zadaných parametrů

Rovnice

Vzorec

Typickým zadáním složitějších úloh je nějaká soustava rovnic. Technik obvykle tyto zadávací rovnice musí umět sestavit na základě zadání. Rovnice nejčastěji získáme kombinací dvou a více jednoduchých vzorců. Sestavování rovnic je ryze lidská schopnost, při které postupujeme systematicky po krocích, které jsou přehledné a srozumitelné, což se nejlépe ukáže na Úloze 2. V rámci této úlohy je představeno i možný postup řešení této úlohy, respektive soustavy rovnic.

Úloha 2:

Vypočítejte jakou vzdálenost ujela tramvaj mezi dvěma zastávkami, když víte, že ze zastávky nejdříve zrychlovala stálým zrychlením 2 m·s^-2 po dobu 7 s, pak 24 s jela ustálenou rychlostí a nakonec zpomalovala ustáleným zpomalením -2 m·s^-2 do zastavení. Sestavení rovnic této úlohy a jejich řešení je popsáno v následujícím odstavcích označených §1 až §3.

§1:

Sestavení rovnic

x_n jako symbol pro neznámou

Ze zadání úlohy je zřejmé, že výsledná rovnice bude obsahovat minimálně dva typy vzorců, a to vzorec pro výpočet ujeté vzdálenosti při rovnoměrně zrychleném/zpomaleném pohybu a vzorec pro výpočet ujeté vzdálenosti při konstantní rychlosti. Vzorec pro výpočet ujeté vzdálenosti při rovnoměrně zrychleném/zpomaleném pohybu má tvar l=1/2(a·t²) a vzorec pro rychlost na konci rovnoměrného zrychlení z nuly má tvar V=a·t [Macháček, 1995, s. 39], kde l [m] je ujetá vzdálenost; t [s] je čas; V [m·s^-1] rychlost v čase t a a [m·s^-2] je zrychlení (záporné číslo je zpomalení). Celkovou ujetou vzdálenost si označme jako x₁ (písmeno x se používá k označení veličin, které nejsou známy, respektive nejdou jednoduše ze zadání vyčíst), vzdálenost při rovnoměrném zrychlení x₂, vzdálenost ujetou konstantní rychlosti x₃ a vzdálenost ujetou při zpomalování x₄. Je evidentní, že celková vzdálenost x₁ bude součtem vzdáleností x₂, x₃, x₄ a x₅, viz soustava rovnic 27.

27:

x₅ [m·s^-1] rychlost tramvaje na konci zrychlování – je označena písmenem x, protože je to také neznámá.

Soustava rovnic

Parametry rovnice

Podmínka řešitelnosti

Výsledná skupina rovnic se nazývá soustavou pěti rovnic o pěti neznámých. Konstanty v rovnicích označujeme jako parametry rovnice. Sestavená soustava rovnice má řešení pouze tehdy rovná-li se počet neznámých počtu dostupných rovnic a

TECHNICKÁ MATEMATIKA

1.24

současně jsou všechny rovnice na sobě nezávislé, tj. žádnou z rovnic nelze odvodit ze zbývajících. Ale naopak velmi často můžeme mít k dispozici více rovnic než neznámých, pak vybereme pro řešení počet rovnic odpovídající počtu neznámých.

§2:

Numerické řešení

Nyní jsou v podstatě dvě možnosti jak dosáhnout požadovaného výsledku neboli řešení těchto pěti rovnic. Myšlenkově nejméně náročné je postupně vypočítat jednotlivé neznáme dosazením hodnot za zrychlení a čas (vyčíslení neznámých x₄, x₃ a dosazením do první rovnice pro x₁ její výpočet), jak je již naznačeno při zápisu rovnic – takovýto postup se nazývá numerické metoda či řešení. Druhou možností je z těchto pěti rovnic udělat jen jednu, respektive vytvořit relativně složitý vzorec pro přímý výpočet ujeté vzdálenosti tramvaje, takové řešení se označuje také jako obecné.

§3:

Obecné řešení

Obecné řešení je výsledek algebraických úprav rovnic, při kterém soustavu rovnic převedeme na vzorce ve formě x₁=.... Takový vzorec vznikne tzv. postupným dosazováním do první rovnice, kdy za jednotlivé neznámé x₂...x₅ se dosazují rovnice pro jejich výpočet, tak aby na pravé straně nebyla žádná neznámá, viz postup uvedený na Obrázku 28, kde je výsledku dosaženo prakticky jen ve dvou krocích.

28:

Obecné řešení soustavy Rovnic 27.

Numerické vs. obecné řešení

Nevýhodou výsledného Vzorce 28 (v tomto případě nás zajímalo řešení jen proměnné x₁) je, že nejsou okamžitě patrny mezivýsledky, které bývají u složitějších úloh důležité, protože z nich plyne celková představa o situaci a lépe se hledají ve výpočtu případné chyby a jsou patrné vlivy jednotlivých členů na výsledek, například jestli při zvyšování hodnoty jedné veličiny ujetá vzdálenost klesá nebo naopak roste atd.

Obecná řešení rovnic

Algebraické úpravy

Separace

Osamostatňování

Základem nalezení obecného řešení rovnic/e jsou algebraické úpravy. Ty spočívají postupných úpravách rovnic, tak abychom separovali, respktive osamostatnili vyšetřovanou neznámou, například u rovnice 2,54 + a = b·x²+(2x²+c)d je potřeba separovat neznámou x. To se dělá vhodnými promyšlenými algebraickými operacemi, při kterých musí být zachována rovnost pravé a levé strany rovnice.

TECHNICKÁ MATEMATIKA

1.25

Například, přičítáním stejného čísla k pravé i levé straně rovnice tak, aby byla zachována její rovnost. To samé pravidlo platí i pro jiné matematické operace včetně umocňování, logaritmování atd. Postup separace neznámé x je zobrazen na Obrázku 29.

29:

V tomto případě stačilo 6 kroků a výpočet veličiny x už nebude problém. Do uvedených šesti kroků jsem zahrnul i zjednodušování rovnice, například kroky 2 a 3 zkušení výpočtáři slučují apod.

Substituce

Především při úpravách je dobré rovnici co nejvíce zjednodušit, taky abychom se v ní neztráceli a nemuseli neustále opisovat spoustu symbolů. Například během úprav Rovnice 29 lze x² označit zkráceně například symbolem y a v kroku 5 opět dosadit x², tomu se říká substituce. Také se může vyskytnout logaritmická rovnice a místo x² v předchozí rovnici může být například log 2x opět by šlo za tento výraz při úpravách dosadit symbol y a v pátém kroku dosadit zpět log 2x apod.

Kanonický tvar rovnice

Obecná řešení

Pro mnoho typů rovnic, které řešíme už vyřešené byly a je známo jejich obecné řešení, které lze velmi rychle transformovat pro naše potřeby. Takové obecné řešení vyšetřované soustavy rovnic nalezneme pouze ve dvou krocích. Nejprve převedeme vyšetřované rovnice na tzv. kanonický tvar, což je jakýsi normalizovaný zápis rovnice. Následně pro výsledné kanonické tvary odečteme obecné řešení z dostupného souhrnu matematických vzorců.

Lineární rovnice

Exponenciální rovnice

Kanonické tvary lineárních a exponenciálních rovnic s celými exponenty jsou uvedeny na Obrázku 30. Samozřejmě parametry a, b mohou být a také v praxi často bývají rovny nule, takže rovnice x³+C=0, kde C je konstanta, je stále kubická rovnice a její kanonický tvar je 1·x³+0·x²+0·x¹+C=0,.

30:

vlevo kanonické tvary lineárních rovnic (bez exponentů); vpravo kanonické tvary polynomů druhé, třetího až n-tého stupně (pro n≥1) – neboli kvadratická, kubická rovnice atd. a₂₁ znamená, že se jedná o konstantu z druhého řádku před první neznámou.

TECHNICKÁ MATEMATIKA

1.26

Odtud lze snadno stanovit kanonický tvar soustavy rovnic 27 a kvadratické Rovnice 29, které jsou uvedeny na Obrázku 31.

31:

vlevo kanonický tvar soustavy Rovnic 27. vpravo kanonický tvar kvadratické Rovnice 29.

Obecná řešení lineárních rovnic

Obecné řešení lineární rovnice o jedné a dvou neznámých je uvedeno na Obrázku 32, obecná řešení kanonických tvarů soustav lineárních rovnic o více jak dvou neznámých se už obvykle neuvádí, protože jsou velmi rozsáhlá, ale principiálně lze odvodit obecné řešení pro libovolně rozsáhlou soustavu lineárních rovnic, ale výsledné vztahy by byly také rozsáhlé velmi nepřehledné. Proto se u soustav lineárních rovnic větších jak 3 (kromě triviálních případů) se používá mechanická numerická metoda řešení, viz kapitola Numerická řešení rovnic.

32:

vlevo obecné řešení lineární rovnice o jedné neznámé; vpravo obecné řešení soustavy dvou lineárních rovnic. Obě řešení jsou pro kanonický tvar. Obecné řešení soustavy dvou lineárních rovnic je odvozeno v Příloze 17.

Obecná řešení exponenciálních rovnic

Niels Abel

Kvadratická rovnice

Kořeny kvadratické rovnice

U polynomů existuje obecné řešení pro rovnice alespoň do n=4 (důkaz provedl norský matematik Niels Abel (1802-1829) [Mareš, 2006, s. 85]), tato řešení jsou uvedena v každém přehledu matematických vzorců, například v [Rektorys et al., 2003, s. 38]. Na Obrázku 33 je uvedeno obecné řešení pro rovnici kvadratickou, která se v technické praxi vyskytuje velmi často. Jak je patrné kvadratické rovnice mohou mít dvě řešení (tzv. kořeny), přičemž obvykle je jeden záporný a jeden kladný, ale technik hledá pouze jedno, a tak v takových případech vybírá to, které lépe vyhovuje očekávání (obvykle je to ten kladný kořen) a takový výsledek dává smysl.

33:

Obecné řešení kvadratické rovnice: D tzv. diskriminant. Pokud bude diskriminant menší než nula D<0, pak má kvadratická rovnice komplexní kořeny (výsledkem je komplexní číslo).

TECHNICKÁ MATEMATIKA

1.27

Numerická řešení rovnic

K numerickému řešení rovnice se přistupuje například tehdy je-li úpráva rovnice příliš duševně náročná nebo nemožná a u větší soustavy rovnic, u kterých se z praktických důvodů na hledání obecného řešení rezignuje. Numerické řešení je jedinou cestou u rovnic 5 stupně a obecně rovnice, u kterých nelze separovat neznámou, respektive nejsme schopni odvodit obecné řešení v přímém tvaru, viz Rovnice 34.

Iterační výpočet

Rovnic 34 je zvláštní v tom, že nelze získat algebraickými úpravami její obecné řešení a jediná možnost nalezení řešení je iterační postup. Na počátku iteračního výpočtu obvykle odhadneme (na základě dostupných dat) interval na ose čísel, ve kterém by se mohl nalézat očekávaná hodnota hledané neznámé a postupně testujeme možná řešení – při iteračních postupech často nejsme schopni dosáhnout zcela přesného výsledku, ale výsledku s určitou přesností. Iterační metod je velké množství, ale téměř vždy jsou založeny na derivacích funkcí (viz [Rektorys et al., 2003, s. 603]), takže si řekněme něco jen o základní iterační metodě Monte Carlo založené na odhadu.

34:

Parametry Re, C jsou konstantami. λ veličina, kterou máme vypočítat. V tomto případě se jedná o tzv. Colebrookovu rovnici pro výpočet součinitele tření v potrubí, více v článku Vznik tlakové ztráty při proudění tekutiny a její výpočet [Škorpík, 2023].

Metoda Monte Carlo

Při metodě Monte Carlo náhodně testujeme různá řešení. Obecně se za řešení považuje množina čísel, interval na ose čísel nebo konkrétní číslo, o kterém se předpokládá, že leží blízko řešení. Konkrétně v případě Rovnice 34 by mohl probíhat tak, že bychom nejprve převedli výraz na pravé straně na levou (rovnice se pak bude rovnat nule), při následném testování výsledků pro různá řešení (námi vybraný interval čísel, o kterém si myslíme, že by mohl obsahovat řešení) pro λ bychom sledovali, jestli se levá strana blíží nule (pak zužujeme interval správným směrem – zvyšujeme přesnost výsledku) a nebo vzdalujeme od nuly (pak interval možných řešení rozšiřujeme), viz Úloha 3. Je zřejmé, že metoda Monte Carlo je nejvíce náročná na počet výpočtových kroků, ale s nástupem počítačů se jedná o velmi používanou metodu a využívá se dost často pro hledání řešení i mnohem méně náročných rovnic např. 3·x+1=7, protože rychlost stolních počítačů je vysoká a šetří tak duševní úsilí výpočtáře a navíc metodu výpočtu obsahují i kancelářské tabulkové procesory.

Úloha 3:

Iterační výpočet

Řešte Rovnici 34 metodou Monte Carlo, pro parametry Re=4·10⁵, C=6,6667·10^-3. Řešení úlohy je uvedeno v Příloze 3.

TECHNICKÁ MATEMATIKA

1.28

Postup řešení Úlohy 3

zadání:

Re; C

výpočet:

hodnot levé strany rovnice z ř. 2 pro vybrané hodnoty λ z intervalu definovaného v ř. 3

úprava:

úprava rovnice, tak aby na levé straně rovnice byla 0

porovnání:

výběr výsledku z ř. 4, který je nejblíže hodnotě 0

odhad:

intervalu, ve kterém očekáváme správnou hodnotu neznámé λ

Numerické řešení soustavy lineárních rovnic

Asi si dokážeme představit, že existují rozsáhlejší soustavy rovnic s více neznámými, než je soustava rovnic na Obrázku 31 (například především při řešení schémat v elektrotechnice i schémat rozsáhlých potrubních tras technologických celků, viz například článek Parní turbína v technologickém celku). Takové soustavy řešíme numericky pomocí maticového počtu. Metod na maticové řešení soustavy lineárních rovnic je více [Dobrovolný and Žďárek, 1954, s. 61], [Rektorys et al., 2003, s. 32], [Schmidtmayer, 1967, s. 196], ale asi nejoblíbenější je tzv. Gaussova eliminační metoda a navíc se na ní dobře demonstruje funkce maticového zápisu rovnic.

Gaussova eliminační metoda

Schodovitý tvar

Princip GEM spočívá v tom, že z původní soustavy rovnic vytvoříme prakticky nové rovnice se stejnými výsledky (v rozsahu zaokrouhlování), přičemž výsledná soustava rovnic bude mít v normalizovaném tvaru zleva postupně na každém řádku o jeden nulový parametr navíc, jak ukazuje Rovnice 35. Takže na posledním řádku soustavy je výsledek poslední neznámé, tu následně dosadíme do předposlední rovnice a získáme hodnotu předposlední neznámé atd. O výsledné matici, která obsahuje nenulové parametry pouze na diagonále říkáme, že má schodovitý tvar zleva i zprava.

35:

Cílová soustava rovnic při řešení Gaussovou eliminační metodou

Tato soustava má stejné řešení jako původní soustava Rovnic 30 (hodnoty parametrů b mohou být samozřejmě jiné než v původní soustavě).

Algebraické úpravy

Nové rovnice z původní soustavy tvoříme odečítáním rovnic od sebe, pokud před touto operací odečítanou rovnici vynásobíme takovým číslem, aby výsledná rovnice obsahovala alespoň o neznámou méně na té správné pozici (eliminovaly jsme jednu neznámou), pak se nám postupně podaří dalšími takovými operacemi získat cílový tvar soustavy, viz příklad na Obrázku 36.

TECHNICKÁ MATEMATIKA

1.29

Rovnice lze za účelem rychlejšího výpočtu prohazovat z jednoho řádku na jiný a to lze provádět i se sloupci, ale v takovém případě musíme myslet na to, že pořadí neznámé už nebude odpovídat číslu sloupce (proto dáváme přednost prohození řádků, pokud to jde). Samozřejmě při operacích nelze násobit nulou, proto při výběru dvojice rovnic, které budeme od sebe odečítat, musíme vybrat rovnice takové, abychom nemuseli násobit nulou.

36:

Příklad postupu Gaussovy eliminační metody

Soustavu (b) získáme tak, že poslední rovnici vynásobíme podílem a₁₁·a^-1₂₁, tedy zlomkem 1/3, abychom získali stejnou hodnotu parametru před neznámou x₁ jako v předchozí rovnici. Následně druhou rovnici nahradíme rovnicí, která vyjde odečtením druhé rovnice od první. Soustavu (c) získáme tak, že první rovnici vynásobíme podílem a₂₂·a^-1₁₂, tedy zlomkem 2/(3·2), abychom získaly stejnou hodnotu parametru před neznámou x₂ jako v následující rovnici. Následně první rovnici nahradíme rovnicí, která vyjde odečtením první rovnice od druhé. Výslednou soustavu (d) získáme tak, že první rovnici vynásobíme převrácenou hodnotou parametru a₁₁, tedy číslem -3 a druhou rovnici vynásobíme převrácenou hodnotou parametru a₂₂, tedy zlomkem 3/2.

Homogenní tvar rovnice

Nehomogenní tvar rovnice

Podmínky řešení

Všimněte si, že cílový tvar obsahuje pouze nehomogenní rovnice (lineární rovnice, která má na pravé straně nenulové číslo b≠0), proto je tato eliminační metoda neúčinná, pokud původní soustava rovnic obsahuje pouze homogenní rovnice b=0 – násobením ani odčítáním od sebe se tyto nuly nezmění. Naštěstí stačí, aby alespoň jedna rovnice v původní soustavě byla nehomogenní, pak už stačí vytvořit novou soustavu tak, že ke každé homogenní rovnici přičteme/odečteme onu nehomogenní rovnici.

Matice

U velkých soustav rovnic se při neustálém opisování rovnic vynechává znaménko plus, rovná se i označení jednotlivých neznámých x a celá soustava se zapisuje pomocí tzv. maticového zápisu do matice, viz Obrázek 37. Na Obrázku 38 je konkrétní příklad matice a to matice soustavy lineárních Rovnic 31 i s výslednou maticí, která je jejím řešením. U vstupní matice soustavy Rovnic 38 si také všimněte kolik nul obsahuje.

37:

Příklady maticového zápisu soustavy lineárních rovnic

TECHNICKÁ MATEMATIKA

1.30

To je typický charakter matic z praxe (na rozdíl od příkladů z matematiky, kde je většina parametrů nenulová), a proto jejich výpočet lze velmi urychlit vhodným přeskládáním pořadí matic a pořadí neznámých.

38:

Matice pro GEM a výsledná matice Úlohy 1

Všimněte si, že během řešení matice byly přehozeny sloupce neznámých x₂, x₄, protože toto přehození vedlo k rychlejšímu výpočtu (méně potřebných operací). Celý postup je uveden v Příloze 18.

Programovací jazyk

GEM je vhodná pro matematické stroje, jako jsou programovatelné kalkulačky nebo počítače, protože operace potřebné k dosažení výsledku jsou předvídatelné a lze tedy lehce sestavit postup řešení zapsatelný v programovacím jazyce.

Stupně, nebo radiány?

Oblouková míra

Oblouk

Přepona

Průvodič

V technické praxi se velmi často místo jednotky pro velikost úhlu stupeň [°] používá jednotky radián [rad], tzv. oblouková míra. Použití obou jednotek má své opodstatnění. Zatímco v případě stupňů používáme 360 dílnou stupnici tak u radiánů stupnici o velikosti 2π To má výhodu především pro případy, kdy se s úhly dále pracuje navazujících výpočtech (i v jiných než v trigonometrických), protože součin úhlu v radiánech a délky přepony c je délkou oblouku vytvořené přeponou (přepona se v takovém případě nazývá průvodič), viz Obrázek 39. Takže při pootočení průvodiče o celou otáčku bude délka oblouku rovna obvodu kruhu 2π·c, proto plný úhel v radiánech je roven právě 2π=360°. Podobně oblouk vytvořený pootočením průvodičem

39:

Úhel v radiánech násobený délkou průvodiče c je roven velikosti oblouku kružnice o poloměru c.

TECHNICKÁ MATEMATIKA

1.31

o čtvrt otáčky musí být velký jako čtvrt kruhu 2π·c/4, takže π/2=90° apod. Převod stupňů na radiány je potom jednoduchý X/(2π)=x/360, kde velké X je úhel v rad a x ve stupních, viz. také Převodník 40.

40:

Převodník stupňů na radiány

Technická dokumentace

Kótování úhlů

A proč tedy používáme i stupně? Pro výpočet oblouku pomocí zadaného úhlu ve stupních je sice nutné tyto úhly převést na radiány, ale jednotky stupně mají výhodu ve velmi jemné stupnici a důležité úhly jako pravý úhel 90°, ostrý úhel 45°, přímý úhel 180° a další frekventované úhly 30° a 60° jsou celá čísla. Proto se s dekadickou stupnicí úhlů pracuje mnohem snáz při konkrétních geometrických představách a používají se pro kótování úhlů ve výrobní dokumentaci nějaké součástky, v plánech domů a jiných technických dokumentacích. Radiány ale mají výhodu při širších výpočtech, kdy trigonometrický výpočet je součástí rozsáhlejšího výpočtu a úhly jsou vstupem i do jiných výpočtů (velikosti oblouku, úhlové rychlosti apod.).

Využití totálního diferenciálu neboli přírůstku funkce při popisu nějakého fyzikálního děje

Vyšší matematika

Diferenciální počet

Integrální počet

Předpokládám, že čtenáři se už setkali s diferenciálním počtem, pokud ne, doporučuji knihu Co je a k čemu je vyšší matematika [Rektorys, 2001]. Na středoškolské úrovni se většinou student dozví, mimo pravidel pro derivování a integrování, jak pomocí diferenciálního a integrálního počtu určí délky křivek, velikost ploch a objemy různých objektů. Většinou také něco o určení tzv. extrémů funkce. To jsou věci, o kterých zde psát nebudu (viz obsah knihy výše), navíc drtivá většina řešení jako délky frekventovaných křivek, ploch a objemů objektů v technice je široce dostupná na internetu i v tabulkách. V této kapitole se chci tedy zaměřit na popis podstaty totálního diferenciálu neboli přírůstku funkce při sestavování tzv. diferenciálních rovnic popisující nějaký vyšetřovaný děj a začnu pojmem parciální derivace.

TECHNICKÁ MATEMATIKA

1.32

Parciální derivace

Derivace funkce j-proměnných

Gradient funkce

Přírůstek funkce (Totální diferenciál)

∂ značka pro parciální derivaci

V technice a fyzice se často vyskytují veličiny, které jsou funkcí více nezávislých proměnných a právě takových funkcí se týká parciální neboli částečná derivace. Například pro u=f(x, y) je veličina u funkcí dvou veličin a to x a y. Takový typ rovnice je možné derivovat podle proměnné x i y, přičemž, když se derivuje podle jedné proměnné, tak druhá je považována za konstantu [Rektorys et al., 2003, s. 395], jinými slovy jsme z funkce f(x, y) vytvořili nejprve dvě funkce u_y=f(x, y=konst.), u_xf(x=konst., y). Výsledkem parciální derivace takové funkce je soustava dvou rovnic, viz Rovnice 41). Taková soustava rovnic se využívá například při hledání gradientu skalárního pole nebo přírůstku funkce známé jako totální diferenciál – oba tyto matematické pojmy mají své vlastní kapitoly uvedené v další části článku. Obecně platí, jestliže funkce obsahuje j počet nezávisle proměnných, potom výsledkem parciální derivace takové funkce bude soustava s j rovnicemi.

41:

(a) označení parciální derivace pomocí písmene d (dolní index označuje, která proměnná je při derivaci konstantní) jako značky pro diferenciál [Dobrovolný and Žďárek, 1954, s. 189]; (b) pro přehlednost se upouští od indexů a pro označení parciální derivace se používá místo písmene d znak ∂ (partial).

Pravidla derivování

Pro parciální derivace přirozeně platí stejná pravidla derivovaní jako pro funkce jedné proměnné, a parciální derivace má i stejnou interpretaci (jedná se o směrnici tečny k průběhu funkce ve směru osy proměnné podle, které se derivuje). To znamená, že uvedené dvě parciální derivace v určitém bodě soustavy souřadnic u-x-y představují dvě tečny k této ploše vytvořenou původní funkcí f(x, y) dvou proměnných.

Hmotnostní tok tryskou

Průtokový kužel trysky

Vlastnosti a postup při parciální derivaci lze dobře předvést na příkladu jednoho z nejznámějších vztahů v termodynamice, což je rovnice pro hmotnostního tok ideálního plynu tryskou při podzvukových rychlostech, viz Úloha 4. Tato rovnice obsahuje dvě proměnné a to tlak před tryskou a za tryskou, proto výsledkem parciální derivace budou dvě rovnice. Jedna rovnice bude udávat jak se bude měnit průtok tryskou, když se bude měnit tlak před tryskou a druhá jak se bude měnit průtok, když se bude měnit tlak za tryskou. Výsledkem je prostorová plocha označovaná jako průtokový kužel trysky.

Úloha 4:

Aplikace parciální derivace

Proveďte parciální derivaci rovnice pro hmotnostní tok ideálního plynu tryskou podzvukovou rychlostí. Rovnice je uvedena například v článku Proudění plynů a par tryskami [Škorpík, 2023c]. Předpokládejte konstantní celkovou teplotu plynu před tryskou. Řešení úlohy je uvedeno v Příloze 4.

TECHNICKÁ MATEMATIKA

1.33

m [kg·s^-1] hmotnostní tok plynu tryskou; p_e [Pa] tlak na výtoku z trysky (exit); p_is [Pa] celkový tlak na vstupu do trysky (input); a, b, c, d, e konstanty; m_max [kg·s^-1] maximální tok plynu tryskou, při kterém přestává reagovat na další snižování protitlaku p_e.

Válcová soustava souřadnic

Parciální derivace v jiné soustavě souřadnic už může být trochu složitější, protože diferenciály musíme transformovat. Například pro válcovou soustavu souřadnic se parciální derivace provádí podle proměnných r (poloha na průvodiči), u (délka oblouku od jeho počátku) a a (poloha na ose od jejího počátku) a protože diferenciál v obvodovém směru lze vyjádřit jako součin délky průvodiče a diferenciálu úhlu θ tj. du=r·dθ je ve jmenovateli derivace podle úhlu θ součin r·dθ, viz Vzorec 42.

42:

Derivace funkce k=f(r, ν, a) ve válcové soustavě souřadnic

Vzorce ukazují parciální derivace veličiny k, kterou lze vypočítat pomocí funkce k=f(r, u, a) ve válcové soustavě souřadnic.

Totální diferenciál aneb přírůstek funkce

Klasická úloha v technice je určení infinitezimální změny sledované veličiny, která je funkcí více proměnných, když dojde ke změnám těchto proměnných. Tuto změnu označujeme jako totální diferenciál neboli přírůstek funkce, což je součet změn (diferenciálů) od jednotlivých proměnných. Například kdybychom chtěli vědět o jakou diferenci se změní průtok tryskou z Úlohy 4 (tedy chceme znát totální diferenciál dm), jestliže se změní oba tlaky před i za tryskou o diferenciály dp_is, respektive o dp_e, pak bychom museli nejprve stanovit diferenciál hmotnostního toku od změny tlaku p_is a tlaku p_e, tedy diferenciál dm_pis, respektive dm_pe. Totální diferenciál dm je pak součtem těchto změn. Právě tento výsledný diferenciál se nazývá totálním diferenciálem nebo také přírůstek funkce dvou a více proměnných.

Obecná rovnice totálního doferenciálu

Parciální přírůstek

Obecně lze říci, že totální diferenciál veličiny u, která je dána funkcí f(x, y) dvou proměnných x, y (u=f(x, y)) bude du. Totální diferenciál du představuje přírůstek funkce ve vyšetřovaném bodě (ve kterém jsou známy parciální derivace)

TECHNICKÁ MATEMATIKA

1.34

třírozměrné soustavě souřadnic u-x-y, jestliže se změní velikost proměnných o diferenciály dx, dy, což je graficky znázorněno na Obrázku 43. Rovnici pro totální diferenciál lze dále upravit na tvar du=du_y/dx·dx+du_x/dy·dy=∂u/∂x·dx+∂u/∂y·dy. Takový součet platí i pro funkce s více jak dvěma proměnnými [Rektorys et al., 2003, s. 396], viz obecná Rovnice 44 pro totální diferenciál.

43:

Grafické znázornění totálního diferenciálu: V tomto případě se jedná o funkci u=f(x, y) jejíž přírůstek ve směru x je klesající du_y<0 a ve směru y rostoucí du_x>0. Totální diferenciál neboli přírůstek funkce v okolí vyšetřovaného bodu P je tedy součtem přírůstků v jednotlivých směrech (parciálních přírůstků) du=du_y+du_x.

44:

Totální diferenciál funkce j-proměnných, kde j je počet proměnných a n označuje proměnnou.

Mechanika kontinua

Elementární krychle

A nyní k praktickým příkladům užití totálního diferenciálu. V Úlohách 5 a 6 naleznete příklady odvození rovnic pro totální diferenciál hmotnostního toku, ale zde využití totálního diferenciálu ještě nekončí. Pravidla pro totální diferenciál lze totiž využít při sestavování diferenciálních rovnic a v mechanice kontinua se aplikuje na tzv. elementární krychli, viz Obrázek 45. Teorie elementární krychle se využívá k popisu rovnováhy a změn vyšetřovaných veličin, například sil, energie, tlaku, teploty atd. Na Obrázku 45 je takto stanoven přírůstek nějaké obecné fyzikální veličiny u, který stačí nahradit symbolem pro vyšetřovanou veličinu, například tlakem, teplotou, silou atd.

45:

Elementární krychle v mechanice kontinua

Přírůstek veličiny u v jednotlivých směrech vepsaný do elementární krychle.

Úloha 5:

Přírůstek funkce

Určete totální diferenciál průtoku plynu tryskou. Využijte poznatků z Úlohy 4. Řešení úlohy je uvedeno v Příloze 5.

První krok při řešení Úlohy 5

TECHNICKÁ MATEMATIKA

1.35

Úloha 6:

Přírůstek funkce

Určete totální diferenciál rovnice kontinuity proudění tekutiny v kanále. Rovnice má tvar A·ρ·V=m, kde A [m²] je průtočný průřez kanálu, ρ [kg·m^-3] je hustota, V [m·s^-1] rychlost tekutiny, m [kg·s^-1] je hmotnostní průtok, který je konstantní po celé vyšetřované délce kanálu. Řešení úlohy je uvedeno v Příloze 6.

První krok při řešení Úlohy 6

Užití gradientů při popisu změn sledované veličiny v prostoru

Gradient

Vektor

Gradient teploty

Gradient je vektor v klasickém prostoru a udává změny a jejich směr vyšetřované veličiny ve vyšetřovaném objemu, který označíme jako oblast . Takže například souřadnice gradientu teploty vody v určitém bodu v rybníce by se pro směr x stanovil jako podíl změny teploty v tomto směru Δt_x a vzdálenosti Δx ve směru x, na kterém se tato změna projeví, což se zapíše takto: Δt_x/Δx, kde t [°C] je teploty. Pro směry y a z podobně. Výsledkem jsou tedy tři souřadnice tohoto gradientu, respektive vektoru a^→, které se zapíší tak jako je to na Obrázku 46 vlevo. V tomto případě nám vektor říká o kolik stupňů Celsia se zvýší teplota vody při pohybu daným směrem o vzdálenost 1 m. Aby bylo zřejmé, že tento vektor je gradientem nějaké vyšetřované veličiny, tak se označuje zkratkou grad t, tak jak je uvedeno na Obrázku 52 vpravo.

46:

Příklad zápisu gradientu teploty v objemu rybníku: t [°C] teplota vody; a^→ vektor.

Oblast Ω

Skalární pole

Vektorové pole

Hladina skalárního pole

Prostor, ve kterém stanovujeme gradienty vyšetřované veličiny označujeme jako oblast Ω. Celou oblast Ω můžeme označit jako skalární pole, pokud budeme mluvit o hodnotách teploty v jednotlivých bodech této oblasti, nebo vektorové pole, pokud budeme hovořit o jejich gradientech. Plochy v oblasti Ω, na kterých je vyšetřovaná skalární veličina konstantní se označují jako hladiny skalárního pole.

Směr gradientu

Gradient potenciální energie

Směr gradientu lze v některých případech určit triviálním způsobem. Například směr gradientu potenciální energie vody v nějaké nádobě bude proti směru gravitačního zrychlení (ve směru kolmém na hladinu bude ode dna potenciální energie vody růst), protože potenciální energie je definována vzorcem e=-g·y, viz Obrázek 47. Hladiny skalárního pole budou kolmé na tento směr (jsou rovnoběžné z hladinou vody v této nádobě). Vektory ve vektorovém poli tvořené gradienty budou směřovat ke dnu nádoby. Směr gradientu tepelného toku bude směřovat od teplého ke studenému konci oblasti Ω.

TECHNICKÁ MATEMATIKA

1.36

47:

Gradient potenciální energie vody v nádobě

e [J·kg^-1] potenciální energie 1 kg vody; grad e [J·kg^-1·m^-1] gradient potenciální energie (směr růstu potenciální energie ve vyšetřovaném bodě a jeho velikost v závislosti na souřadnici) v bodě P; g^→ [m·s^-2] gravitační zrychlení g^→(0;-9,81;0). Vyšetřovaná oblast Ω je celý objem vody v nádobě.

Rovnice zachování

Gradient energie

Hydrodynamika

Pro praxi je definice gradientů užitečná také při zápisu rovnic zachování ať už hmoty nebo energie. Na Obrázku 48 příklad rovnice zachování energie tekutiny ve vyšetřovaném objemu Ω. Podle prvního zákona termodynamika může tekutina obsahovat již zmíněnou potenciální energii e, ale i kinetickou V²/2, tlakovou p/ρ a vnitřní tepelnou energii u, které se mohou mezi sebou transformovat. Jestliže na vstupu (označení i) do tohoto vyšetřovaného objemu je všude energetický obsah tekutiny stejný, pak musí v objemu Ω platit, že klesá-li v nějakém směru gradient jednoho druhu energie, tak v tom samém bodě a směru musí gradient jiné energie růst apod. Jinými slovy součet gradientů těchto energií musí být roven nule. Pokud roven nule není, pak to jednoduše znamená, že tato tekutina sdílí energii se svým okolím, což je možné, buď ve formě práce w, nebo tepla q. Toto tvrzení lze tedy zapsat Rovnici 48. Pomocí takové rovnice lze následně vyšetřit proudění po libovolné proudnici mezi vstupem a výstupem, respektive určit jak se mění tlaky, určit vykonanou práci atd., viz také Úloha 8. Tato rovnice je naprosto klíčová rovnice pro studium mechaniky kontinua a v různých obměnách ji obsahují téměř všechny energetické rovnice známe v hydromechanice i Navier-Stokesova rovnice.

48:

Ω-vyšetřovaný objem. e [J·kg^-1] měrná potenciální (energie 1 kg tekutiny); p [Pa] tlak; q [J·kg^-1] měrné teplo sdílené s okolím (může se jednat o teplo přiváděné/odváděné do/z pracovní tekutiny přes hranici vyšetřovaného objemu nebo i o teplo vzniklé/spotřebované chemickou reakcí uvnitř vyšetřovaného objemu); u [J·kg^-1] měrná vnitřní tepelná energie; V [m·s^-1] rychlost tekutiny ve vyšetřovaném boděV_i [m·s^-1] rychlosti proudění na vstupech do vyšetřovaného objemu; V_e [m·s^-1] rychlosti proudění na výstupech z vyšetřovaného objemu; w [J·kg^-1] měrná vnitřní práce tekutiny; ρ [kg·m^-3] hustota tekutiny.

TECHNICKÁ MATEMATIKA

1.37

Gradient tlaku v potrubí

Zápis pomocí gradientů je velmi přehledný pro nalezení různých kontextů i při řešení složitých problémů. Například aplikací poslední Rovnice 48 na proudění kapaliny vodorovným potrubím konstatního průřezu, ve kterém tekutina nekoná práci ani nesdílí teplo s okolím, zjistíme, že klesá-li tlak v důsledku vnitřního tření (tlaková ztráta), tak musí růst hodnota vnitřní tepelné energie kapaliny apod.

Gradient potenciální funkce

Potenciální vektorové pole

Jestliže v celém vyšetřovaném objemu Ω je vyšetřovaná veličina u dopočitatelná podle nějaké funkce u=f(x, y, z) a tato funkce je v celé oblasti spojitá (tzn.v každém bodě oblasti Ω má veličina u danou hodnotu – skalár, číslo), pak lze gradient této veličiny spočítat pomocí Rovnice 49. Přesněji přírůstky sledované veličiny v jednotlivých směrech jsou rovny parciální derivacím v těchto směrech. Přičemž funkci u nazýváme potenciální, protože je funkcí pouze polohy, proto také vektorové pole, které je vytvořeno z gradientů potenciálních funkcí označujeme jako potenciální vektorové pole.

49:

Nepotenciální vektorové pole

Proudění s vnitřním třením

Jestliže je oblast Ω vyplněná vektorovým polem, které je gradientem nějaké veličiny, kterou nelze popsat potenciální funkcí, pak o tom poli říkáme, že je nepotenciální. Typické nepotenciální vektorové pole je vektorové pole rychlostí tekutiny s vnitřním třením, viz článek Vnitřní tření tekutiny a vývoj mezní vrstvy [Škorpík, 2023a]. Pokud neexistuje pro vyšetřovanou veličinu spojitá potenciální funkce u=f(x, y, z), pak lze hodnoty gradientů řešit pomocí statistiky, podobnosti (včetně počítačového modelu), měřením apod.

Gradient potenciální energie

Vraťme se nyní ke gradientu potenciální energie ve sklenici vody z Obrázku 47. V tomto případě jsme schopni sestavit funkci pro výpočet potenciální energie v celém objemu vody a to vzorcem: e=-g·y pro g^→(0;-9,81;0), takže dosazením této funkce do Rovnice 49 získáme gradient potenciální energie ve sklenici vody ve tvaru: grad e=a^→(0;9,81;0). Obecně lze pro gradient potenciální energie (při konstantní hodnotě gravitačního zrychlení) odvodit Vzorec 1234.

Vlastnosti gradientů a práce s nimi ve vektorové analýze

Gradient potenciální funkce

Operátor ∇

Pro potřeby vektorové analýzy, respektive práce s gradeintem v rámci širšího výpočtu, se gradient potenciální funkce zapisuje ve formě parciální diferenciální Rovnice 50 (parametry i^→, j^→, k^→ označují, že se současně jedná o souřadnice

TECHNICKÁ MATEMATIKA

1.38

vektoru). Pro, tímto způsobem zapsaným gradientem, platí pravidla vektorové algebry, například [Rektorys et al. 2003, s. 219], [Garaj, 1957].

50:

∇ operátor nabla.

Potenciální proudění

Gradient kinetické energie

Zrychlení

Jedním z příkladů využití parciální diferenciální rovnice pro popis gradientu potenciální funkce v oblasti Ω je potenciální proudění. Potenciálním proudění se označuje idealizované proudění jehož vektor rychlosti vytváří potenciální vektorové pole. Model potenciálního proudění se uplatňuje v hydrodynamice při popisu proudění ideálních tekutin, pro které má velmi dobré výsledky. Na základě Rovnice 50 lze jednoduše dokázat, že zrychlení v potenciálním proudění je dáno gradientem kinetické energie, viz důkaz v Úloze 7 a další Úlohy 8, 9 na výpočet stavových veličin proudu.

Úloha 7:

Gradient kinetické energie

Dokažte, že zrychlení tekutiny je gradientem kinetické energie tekutiny. Uvažujte potenciální proudění. Řešení úlohy je uvedeno v Příloze 7.

Úloha 8:

Zrychlení v potrubí

Určete zrychlení proudu ideálního plynu v potrubí tepelného výměníku. Uvažujte stacionární proudění a vysokou tepelnou vodivost pracovního plynu. Neuvažujte vliv vnějšího zrychlení. Řešení úlohy je uvedeno v Příloze 8.

Zrychlení plynu v potrubí tepelného výměníku

l [m] délka potrubí; V_{i ,e} [m·s^-1] rychlost na vstupu a výstupu z potrubí; Q [W] celkový tepelný výkon předávaný do plynu na úseku potrubí o délce l; q [J·kg^-1·m^-1] získané teplo 1 kg plynu, které získá na délce l; x [m] vzdálenost vyšetřovaného bodu od začátku potrubí.

Úloha 9:

Gradient tlaku v potrubí

Určete gradient tlaku proudu ideálního plynu v potrubí tepelného výměníku, jestliže znáte funkci pro zrychlení. Použijte výsledky z Úlohy 8. Řešení úlohy je uvedeno v Příloze 9.

Přírůstek potenciální funkce

Jednotkový vektor směru

V případě gradientu potenciální veličiny jsou tedy jeho jednotlivé souřadnice parciálními derivacemi této funkce. Při porovnání s Rovnicí 44 pro přírůstek funkce je evidentní, že pro stanovení přírůstku funkce funkce pro u stačí znát gradienty této veličiny a ty vynásobit diferenciály vzdáleností v jednotlivých směrech (pro složku ve směru x diferenciálem dx atd.). Obecně se taková operace zapíše Rovnicí 51.

TECHNICKÁ MATEMATIKA

1.39

51:

Diferenciál ds^→ se nazývá jednotkovým vektorem směru.

Diference potenciální funkce